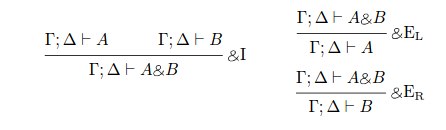AG
Size: a a a
2020 October 23
KV
зачем вайн, если можно просто поставить две системы, и не ебаться ни в одной из них
+++
AG
мультипликативная конъюнкция элиминируется матчингом по всей хурме, а аддитивная - проекциями
AG
с модальностями кстати есть аналогичный феномен
AG
коробка в дуал-контекстной формулировке элиминируется матчингом, а в крипке-стиле - выбором фрейма
R
Сразу начинаешь ощущать себя недоразвитым. (смайлик с подходящим выражением)
R
Скоро заживём
МОСКВА, 23 окт - РИА Новости. "Цифровой рубль может сделать платежи прозрачными и может быть использован для решения социальных задач, например, борьбы с бедностью, заявил в интервью РИА Новости в рамках московского международного форума "Открытые инновации" спецпредставитель президента РФ по цифровому и технологическому развитию Дмитрий Песков."
МОСКВА, 23 окт - РИА Новости. "Цифровой рубль может сделать платежи прозрачными и может быть использован для решения социальных задач, например, борьбы с бедностью, заявил в интервью РИА Новости в рамках московского международного форума "Открытые инновации" спецпредставитель президента РФ по цифровому и технологическому развитию Дмитрий Песков."
"Для того, чтобы пользоваться такого рода цифровыми сервисами, нужен доступ к цифровой инфраструктуре, должны быть две вещи: у вас дома должно быть устройство и должен быть доступ в интернет. На самом деле, это решается достаточно просто - здесь могут быть цифровые посредники. У нас есть, как минимум, две инфраструктуры, которые в стране доходят почти до каждого человека - Сбербанк и "Почта России". Я вполне допускаю, что и получение пенсии, и других платежей может проходить в ситуации, когда бабушка в Иванове приходит на почту и ей там продвинутая девушка на устройстве все показывает и рассказывает, как надо это сделать"
☹️
☹️
AG
Dollar Føølish
Произведение от суммы равно сумме произведений
в данном случае изоморфно
AG
(a, Either b c) ~= Either (a,b) (a,c)VD
да вранье
Не знают нащет вайна, но протон вполне норм. С последним релизом протона у меня на винде остались только vr-игры и то только потому что HTC не сделала дрова для линя.
AG
протон в целом работает, не то чтобы как часы, но скорее да чем нет
VD
А шиндос меня сильно огорчает тем, что после загрузки еще минут 20-30 хрустит винтом как умалишенный и пользоваться им в это время невозможно.
VD
Поэтому вр я последнее время почти не играю, лул.
LO
короче эта херня с плюсами стала валится вообще просто так. похоже таки дело в hs_init
JC
Интересно как с ансейф языками работать
R
Anything that can go wrong will go wrong
LO
https://gitlab.haskell.org/ghc/ghc/-/issues/18601 может оно вот
AG
(a, Either b c) ~= Either (a,b) (a,c)Variables A B C : Prop.
Class Isomorphism A B :=
MkIsomorphism {
from: A -> B;
to: B -> A;
from_to b: from (to b) = b;
to_from a: to (from a) = a
}.
Definition fromPS : A /\ (B \/ C) -> (A /\ B) \/ (A /\ C).
by case=>a; case=>bc; [left|right].
Defined.
Definition toPS : (A /\ B) \/ (A /\ C) -> A /\ (B \/ C).
by case; case=>a bc; split=>//; [left|right].
Defined.
Theorem prodsum : Isomorphism (A /\ (B \/ C)) ((A /\ B) \/ (A /\ C)).
Proof.
have froto (sp : A /\ B \/ A /\ C): fromPS (toPS sp) = sp
by move: sp; rewrite /fromPS /toPS; case; case.
have tofro (ps : A /\ (B \/ C)): toPS (fromPS ps) = ps
by move: ps; rewrite /fromPS /toPS; case=>a; case.
apply: MkIsomorphism froto tofro.
Qed.
AG
как говорится а вот и пруфы подъехали
LO
походу пришло время компилять head на винде