к
если бы не это, можно было бы сделать красивый ромбик)
Size: a a a
2018 February 23
AG
потому что η : I → T
ЗП
это pure/return
ЗП
ЗП
a -> m a
к
снова проблемы чтения нотации, я думал это композиция с Identity-функтором
AG
скорее T(I(X))
к
какой-то ад
AG
таки композиция
к
ну да, осознал
к
все
ЗП
ну правильно же должно быть 2 нат преобразования
I -> M и Compose
I -> M и Compose
ЗП
I a -> M a
ЗП
просто в хаскелл же I a ~ a
к
сигнатура η заставляет добавлять лишний I, я думал он "как-нибудь" сам подставится, в уме
ж
снова проблемы чтения нотации, я думал это композиция с Identity-функтором
кто ты и что ты сделал с каной?
кана же шарит в теоркате
кана же шарит в теоркате
OP
вот и он как раз на сопряжения для лист монады подоспел
Там F-алгебры, это мы не проходили
AG
ну в диаграммах I даже не рисуют, типа невидимая веревочка
ЗП
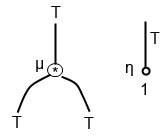
1) это тензорное произведение функторов (Compose)
2) это I -> T
вот вам и моноид в категории эндофункторов
2) это I -> T
вот вам и моноид в категории эндофункторов
ЗП
ну в диаграммах I даже не рисуют, типа невидимая веревочка
я же прав?