Телеграмм чат группы tkhirianov_python

Size: a a a

Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

2279 membersпожаловаться на группу

2020 September 04

НП

Нехристь Пендостанск... in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

Oleg Makarikhin

какой курс? в матанализе есть примерно такое же нотация Ландау. О-большое.

Это скрин из википедии

источник

20:37пожаловаться #1

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

нормальный - у тебя есть некий алгоритм время работы которого зависит от входа n какой то зависимостью - ты хочешь понять - с какой скоростью это время растет при увеличении n

источник

20:43пожаловаться #2

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

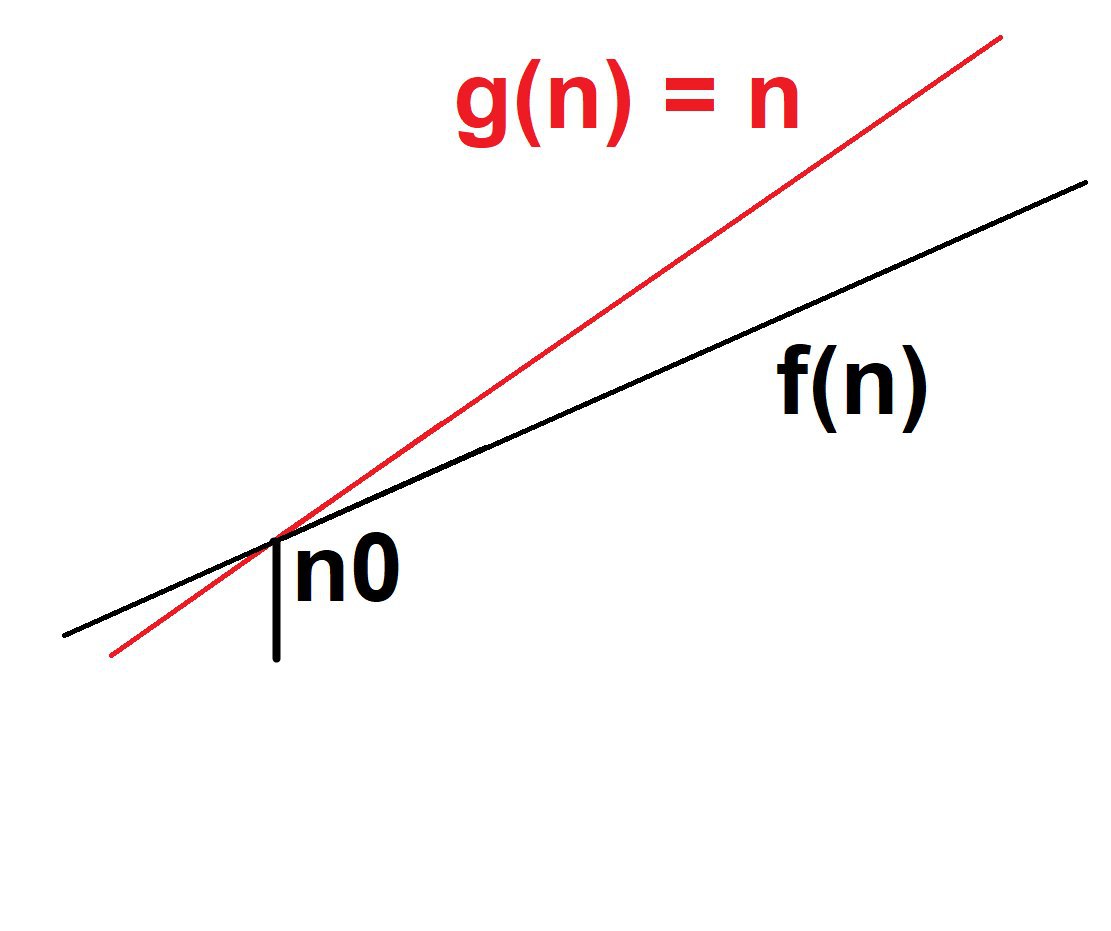
ты пытаешься найти функцию g(n) такую, что для любого n начиная с некоторого - существует число K такое что |f(n)| <=|C*g(n)|

источник

20:50пожаловаться #3

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

источник

20:55пожаловаться #4

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

возьмем, например f(n) и построим график времени от n

источник

20:56пожаловаться #5

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

f(n) может разные наклоны иметь

источник

20:57пожаловаться #6

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

но какой бы она наклон не имела - мы всегда можем домножить g(n) = n на число некоторое

источник

20:58пожаловаться #7

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

что в итоге график C*g(n) начиная с некоторого n0 - точки пересечения - всегда будет выше чем f(n)

источник

20:59пожаловаться #8

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

источник

21:00пожаловаться #9

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

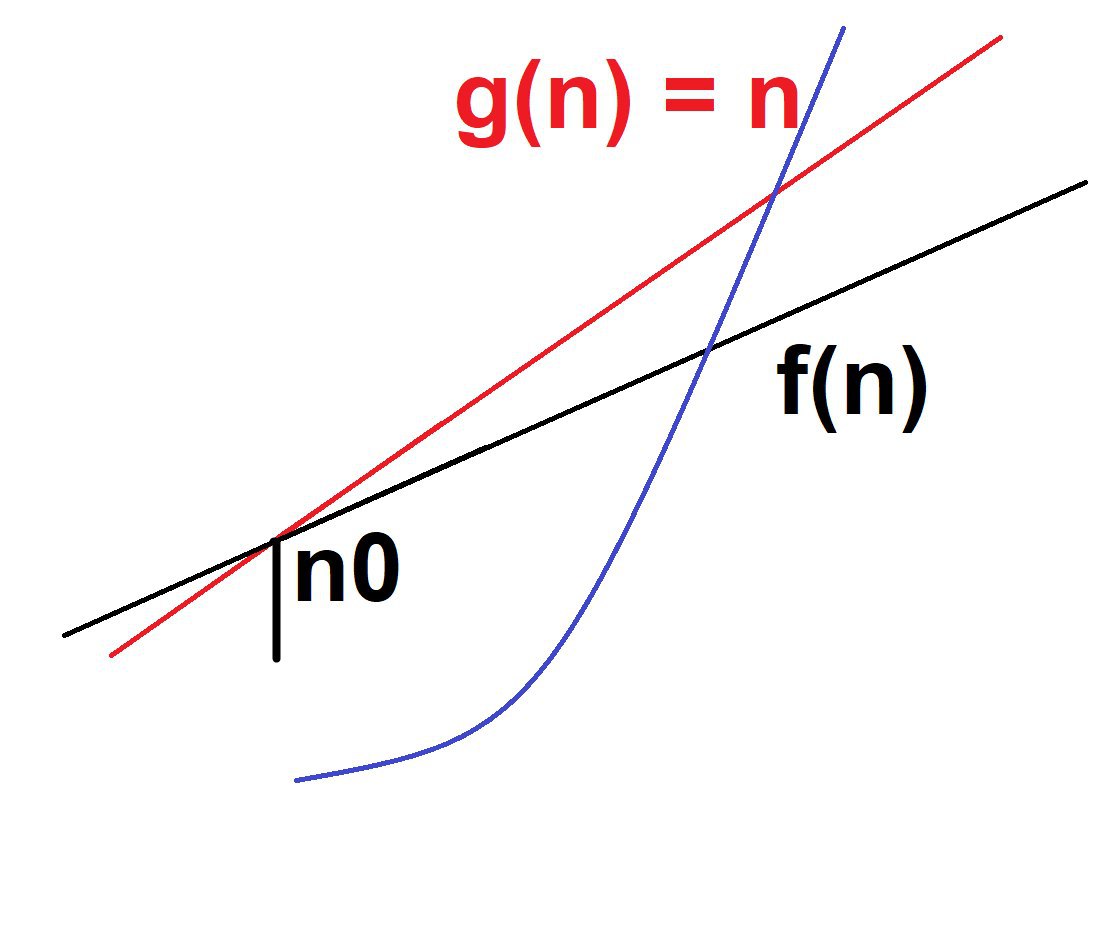
если бы, скажем f(n) была параболой какой то - неважно какой

источник

21:00пожаловаться #10

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

смещенной, растянутой

источник

21:00пожаловаться #11

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

важно то что мы не сможем для g(n) = n найти такой множитель, чтобы графики не пересекались начиная с некоторого n0 и до бесконечности

источник

21:01пожаловаться #12

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

то есть как бы мы не поворачивали или не перемещали прямую красную - мы не сможем сделать так чтобы она на бесконечности была выше чем синяя
синяя в любом случае пересечет прямую любую и будет выше

источник

21:02пожаловаться #13

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

но можем например экспоненту взять - и она будет выше чем парабола на бесконечности

источник

21:06пожаловаться #14

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

то есть как минимум - экспонента ограничивает сверху

источник

21:07пожаловаться #15

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

функции можно представить в виде многочлена в окрестности некоторой выбранной точки - как сумму a0 + ax + bx^2 +cx^3 и тд

источник

21:09пожаловаться #16

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

ну и мы должны найти - начиная с какой степени график может обогнать нашу функцию

источник

21:10пожаловаться #17

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

a0 - нулевая степень - не можем найти
a0 + ax - первая степень - прямая, тоже не можем
a0 + ax + ax^2 - вторая степень - можем
найти такую параболу которая будет обгонять на бесконечности

источник

21:11пожаловаться #18

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

значит сложность ассимптотическая - O(n^2) - это значит что мы можем для исследуемой функции подобрать параболу которая будет на бесконечности обгонять ее

источник

21:15пожаловаться #19

mr.slavik in Хирьянов Т.Ф., Практика программирования на Python 3 (2019)

то есть скорость роста времени работы алгоритма нашего в зависимости от n - не больше квадратичной, какая конкретно - мы не можем сказать заранее, но точно можем сказать, что не больше квадратичной при n стремящимся к бесконечности

источник

21:19пожаловаться #20