D
Size: a a a
2017 January 06
Поиск по сообщениям, которые были раньше
D
До преобразования в суперчатик.
r
да
r
D
А. Не, внутричатиковый поиск
D
Нажми тут Ctrl+F
r
то же самое
D
А, ну у меня нет. Мож, платформозависимо
2017 January 07
IS
Знает кто нибудь где взять доказательство основаное на перестановках?
Пусть M — наша матрица, A — верхняя левая, O — верхняя правая (нулевая), B — нижняя левая, C — нижняя правая клетки
Мы представляем |M| как сумму произведений вида [sgn(t) · a_{1,t_1} · ... · a_{n,t_n}], где t \in S_n
1. Докажи, что если в произведение попадает хоть один элемент из B, то туда попадет элемент из O, и значит оно будет равно нулю. В итоге выйдет, что при подсчете определителя элементы из B не учитываются
2. Докажи, что |M| = |M'|, где M' — почти то же самое, что и M, только с B = O (тоже нулевая матрица)
3. Докажи, что |M'| = |A| · |C|: это делается в лоб — у нас одинаковые слагаемые и справа и слева, нужно только не забыть про знаки перестановок
Мы представляем |M| как сумму произведений вида [sgn(t) · a_{1,t_1} · ... · a_{n,t_n}], где t \in S_n
1. Докажи, что если в произведение попадает хоть один элемент из B, то туда попадет элемент из O, и значит оно будет равно нулю. В итоге выйдет, что при подсчете определителя элементы из B не учитываются
2. Докажи, что |M| = |M'|, где M' — почти то же самое, что и M, только с B = O (тоже нулевая матрица)
3. Докажи, что |M'| = |A| · |C|: это делается в лоб — у нас одинаковые слагаемые и справа и слева, нужно только не забыть про знаки перестановок
NK
А кому писать по поводу админки?
А можно попросить свой homepage на этом сайте сделать?
А можно попросить свой homepage на этом сайте сделать?
o
Поработал с урлами) Теперь можно запинить http://www.zepta.ru/w/Заглавная_страница
2017 January 08
2017 January 09
N
http://math.stackexchange.com/questions/450803/how-prove-this-they-have-a-common-fixed-point
Кто-нибудь доказывал эту задачку?
В комментариях говорят, что в общем случае неверно, но пример не дают.
Кто-нибудь доказывал эту задачку?
В комментариях говорят, что в общем случае неверно, но пример не дают.
N
отображения заданы на отрезках (замкнутых множествах)
может, поэтому в комментариях говорят, что надо уточнить условие
может, поэтому в комментариях говорят, что надо уточнить условие
2017 January 16
IS
http://math.stackexchange.com/questions/450803/how-prove-this-they-have-a-common-fixed-point
Кто-нибудь доказывал эту задачку?
В комментариях говорят, что в общем случае неверно, но пример не дают.
Кто-нибудь доказывал эту задачку?
В комментариях говорят, что в общем случае неверно, но пример не дают.
Это из учебника Зорича за 2015 год: там он уже говорит, что это работает не для всех функций
IS
Но даже при этом уточнении контрпример с f(x) = (x+1)/2, g(x) = (1-x)/2 вроде как все портит
N
лол
спасибо
спасибо
M
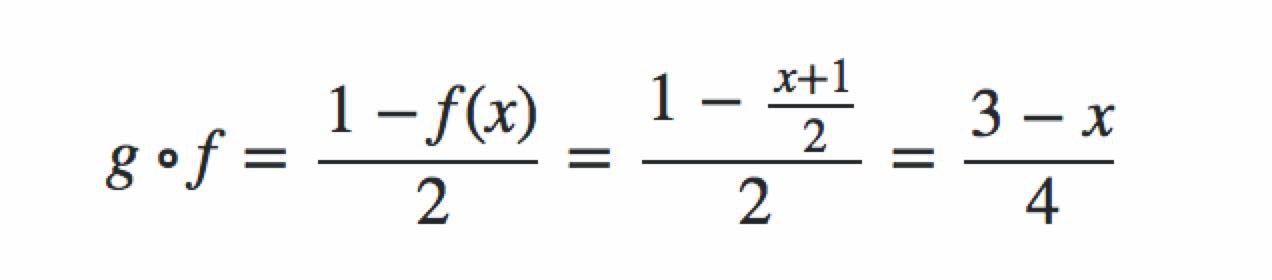
M
в последнем равенстве ошибка