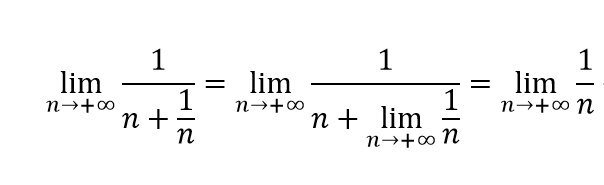доказал?

Нет, с чего вы ызяли, что можете вот так тупо подставить предел?

Как правильно?

Можно о() записать

вам нужно вынести n из знаменателя, тогда у вас получится произведение последовательностей (1/n) и (1/(1 + 1/n^2)), обе эти последовательности сходятся (одна к 0, другая к 1), значит и их произведение сходится

1/(n + 1/n) = n/(n^2 + 1)

Оцениваешь величину справа сверху и снизу и дальше теорема о трех милиционерах

а вообще можно миллионом способов это все доказать

Или так

Я выше написал

мне для этого и нужно упростить. Там потом многодробные выражения, хочу убрать лишние члены, чтобы упростить запись

Типа я операцию деления на выражение применяю несколько раз

ещё можно вспомнить всякие забавные леммы из матана первого курса и заметить, что n + 1/n — сумма бесконечно большой последовательности и ограниченной (потому что 1/n сходится => ограничена), а это снова является бесконечно большой последовательностью => единица, деленная на эту последовательность, является бесконечно малой последовательностью (все законно, т.к. ни один член последовательности не равен нулю, делить можно), а значит сходится

Че?


n/n^3 < n/(n^2 +1) < n/n^2

при n > 1

всем чатом придумали уже 4 разных решения

у меня исходное выражение многоэтажное получается

я задолбаюсь писать все члены

Ну вам накидали методов, берете и используете их

вообще да, тогда получается поэтапное решение

вам не нужны многоэтажные выражения, когда вы разбираетесь с пределами последовательностей, то вы должны внимательно следить за поведением общего члена, вытаскивание слагаемых туда-сюда не всегда помогает, есть примеры задач, показывающих это