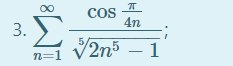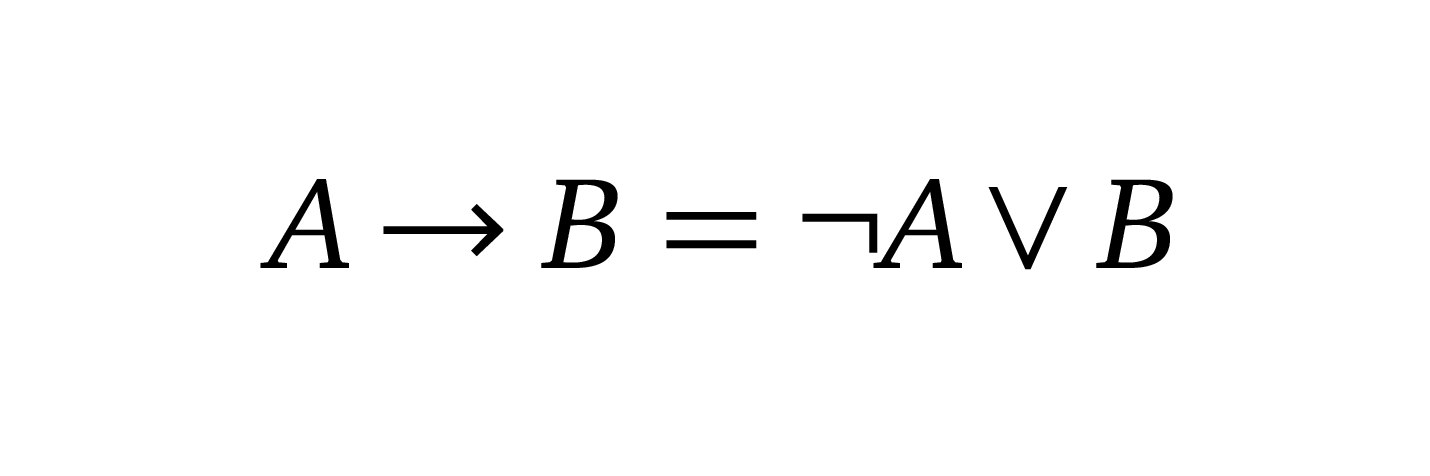mq
Size: a a a
2020 September 20
~ 1/n
G
сводится к гармоническому ряду, который, как мы знаем, расходится
q
согласен, я понял, спасибо
A
а как формально доказать,что если еще добавить импликацию,то любую функцию можно будет выразить?
R
R
(и, или, не) образует полную систему.
A
можно еще как-то словами?
R
Импликацию можно выразить через дизъюнкцию и отрицание; тогда набор (и, или, импликация) сведётся к (и, или, не). Но этот набор — полный, так что и исходный — тоже.
A
Импликацию можно выразить через дизъюнкцию и отрицание; тогда набор (и, или, импликация) сведётся к (и, или, не). Но этот набор — полный, так что и исходный — тоже.
нам не вводили полный набор
R
Полный набор операций (функций) — такой, что через функции, входящие в него, можно выразить любую логическую функцию.
A
а как формально доказать,что если еще добавить импликацию,то любую функцию можно будет выразить?
из импликации получаем отрицание, а далее любую функцию можно привести в КНФ/ДНФ
A
хотя я не знаю, как из импликации получить отрицание
A
только если константа 0 есть
A
ну то есть это в принципе не правда
и, или и импликация сохраняют 1
и, или и импликация сохраняют 1
G
а как формально доказать,что если еще добавить импликацию,то любую функцию можно будет выразить?
нельзя же?
G
по тому же критерию Поста вроде нельзя
A
Полный набор операций (функций) — такой, что через функции, входящие в него, можно выразить любую логическую функцию.

то есть тут можно написать функцию не х или в, а потом черех импликацию выразить
G
набор конйункция, дизйункция и импликация сохраняет единицу, то есть функцию f(1,1)=0 через него не выразить
G
а, туплю, тут по-другому сформулировано, тут надо доказать, что существует функция, которую нельзя выразить только через и и или, но можно с импликацией, а не что можно любую выразить
G
это просто, это будет просто любая функция, которая не сохраняет ноль, но сохраняет единицу