A
Size: a a a
2020 April 10
Бурбаки это большая группа французских математиков
KK
В общем есть прям факт что французы лишь немного в теорию могут, с практикой там огромные проблемы
f
Ну вот современных влиятельных русских/американцев/китайцев/японцев/немцев очень легко вспомнить
Немцев?
KK
Немцев?
Угу
f
Ну вспомните тогда
f
Что-то немцы и не вспоминаются :(
KK
Да хотя бы алсведе
P
В общем есть прям факт что французы лишь немного в теорию могут, с практикой там огромные проблемы
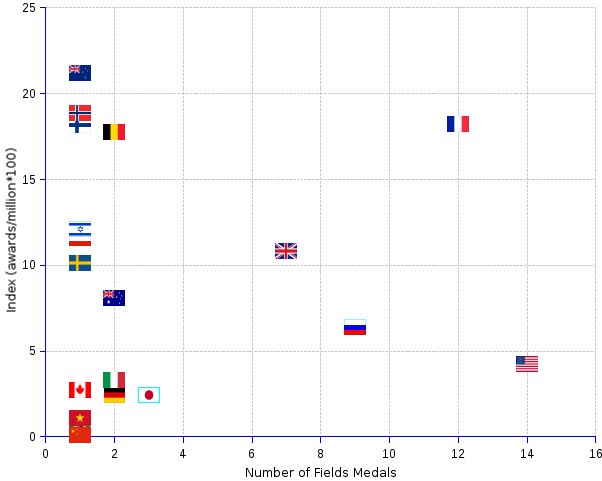
есть прям факт, что если ты откроешь википедию и посмотришь сколько филдсовских медалистов из франции, то с 90х их наверно больше всех, а если за всю историю то... тоже.
KK
есть прям факт, что если ты откроешь википедию и посмотришь сколько филдсовских медалистов из франции, то с 90х их наверно больше всех, а если за всю историю то... тоже.
Целых 2
EZ
Франция сильна в математике? Шо?
P
есть прям факт, что если ты откроешь википедию и посмотришь сколько филдсовских медалистов из франции, то с 90х их наверно больше всех, а если за всю историю то... тоже.
сорян, в США -- 13, Франция 12 сейчас за всю историю
e
Насколько я помню, можно.
Идея в том, что мы храним в фенвике не сам массив, а его частичные разности. Тогда прибавление на прямоугольнике это 4 обновления в точках. А запрос суммы это какая-то аккуратная возня с суммированием арифметических прогрессий (потому что теперь каждая квадратная "клеточка" поля имеет свой вес.
При этом в каждой вершине мы храним не только сумму на ней, но и сумму с коэффициентами (в одномерное случае она выглядит как
a[r] + a[r-1]*2 + a[r-2] * 3 + ... a[l] * (r-l+1), в двумерном как-то похоже).
Идея в том, что мы храним в фенвике не сам массив, а его частичные разности. Тогда прибавление на прямоугольнике это 4 обновления в точках. А запрос суммы это какая-то аккуратная возня с суммированием арифметических прогрессий (потому что теперь каждая квадратная "клеточка" поля имеет свой вес.
При этом в каждой вершине мы храним не только сумму на ней, но и сумму с коэффициентами (в одномерное случае она выглядит как
a[r] + a[r-1]*2 + a[r-2] * 3 + ... a[l] * (r-l+1), в двумерном как-то похоже).
а разве фенвик в матрице не должен хранить в клетке сумму всего прямоугольника?
KK
В иппи столько же
KK
В одном институте)
MB
а разве фенвик в матрице не должен хранить в клетке сумму всего прямоугольника?
Должен
MB
А еще он будет хранить эту же сумму, но с коэффициентами для разных клеток
e
так не совсем понял последней строчки
MB
Так, посмотрим на одномерном случае.
MB
Чтобы посчитать сумму на отрезке [l; r], надо вычислить
a[l] * (r-l+1) + a[l+1] * (r-l) + ... + a[r-1] * 2 + a[r]
a[l] * (r-l+1) + a[l+1] * (r-l) + ... + a[r-1] * 2 + a[r]
e
так это не сума(р)-сума(л-1)?