Oℕ
Size: a a a
2020 February 23
бифунктор - это функтор из произведения категорий
Oℕ
на этой диаграмме прозведение двух объектов, хотя любую категорию можно считать произведением единичной и ещё одной точно такой же, это будет бессмысленным усложнением
МБ
Нужно две индексных категории?
Зачем?
Oℕ
в общем - нет, произведения выражаются самым обычным функтором
AK
Тогда не понимаю как это будет на хаскеле / скале. Например, у меня в I два объекта: String и Int, я хочу их с помощью Дельта цэ певерести в (String, Int). Где у меня ошибка?
Oℕ
Не могу тогда представить его. Допустим у меня есть объекты Ai и Bi в индексной, я их отображаю в A × B
да вы их отображаете в какие-то два возможно разных объекта в ващей категории
МБ
Тогда не понимаю как это будет на хаскеле / скале. Например, у меня в I два объекта: String и Int, я хочу их с помощью Дельта цэ певерести в (String, Int). Где у меня ошибка?
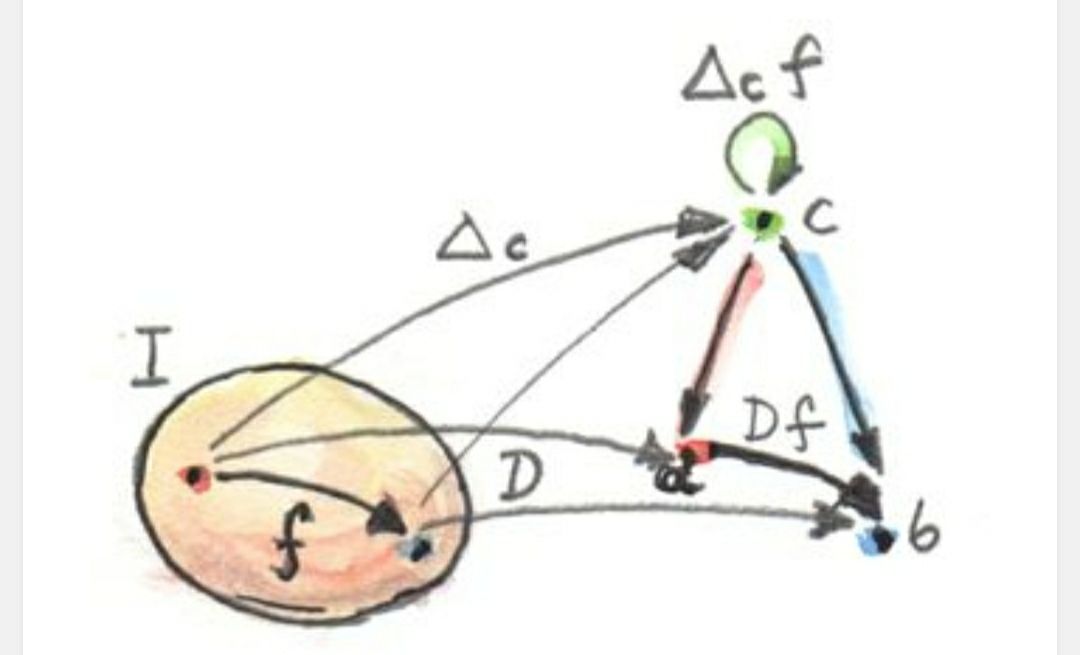
Дэльта Це и не переведёт их в произведение. Произведение будет пределом в категории конусов, которую эти ДельтатЦэ формируют
Oℕ
Тогда не понимаю как это будет на хаскеле / скале. Например, у меня в I два объекта: String и Int, я хочу их с помощью Дельта цэ певерести в (String, Int). Где у меня ошибка?
вы совсем запутались, похоже
в индексной категории в случае произведения пары объектов у вас есть пара объктов, вообще не важно как их назвать, можете назвать их 1 и 2
в индексной категории в случае произведения пары объектов у вас есть пара объктов, вообще не важно как их назвать, можете назвать их 1 и 2
Oℕ
чтобы задать функтор вы отображаете каждый в какой-то объект целевой категории, в вашем случае в типы String и Int
Oℕ
т.к. стрелок, кроме единичных в индексной категории нет, больше ничего задавать не нужно
Oℕ
предел этого функтора и будет объект - тюпл (String, Int) или любой изоморфный ему
Oℕ
ну объект и прилагающийся конус
Oℕ
т.е. функции fst @ String @Int и snd @String @Int
Oℕ
Лимит - это одноразовая или "локальная" конструция, то, что вы построили произведение для заданной пары объектов в общем случае не говорит вам ничего
Oℕ
С другой стороны вы можете иметь произведение глобально - т.е. ваша категория гарантирует, что для любой пары объектов вы можете построить произведение
Oℕ
Как например Set\Hask и т.п.
Oℕ
В таких случаях вот эта глобальная универсальная конструкция произведения любой пары объектов действительно задаёт бифунктор, но уже не из индексных категорий, а из произведения вашей категории на саму себя
AK
А как будет выглядеть функтор дельта?
Oℕ
в каком случае?
Oℕ
мне кажется, в любом обучающем ресурсе про лимиты есть пример диаграммного функтора для произведения