MT
Size: a a a
2020 October 29
Это что-то вроде того, что аксиома выбора есть, но её запрещено использовать на базовом бесконечном множестве
На конечных множествах аксиома выбора и не нужна
CD
На конечных множествах аксиома выбора и не нужна
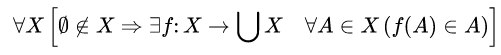
тут добавлено условие "и объединение X не равносоставлено N"
CD
что-то вроде такого
CD
где N - эталонное бесконечное множество
G
Хм... как наличие двух различных пустых множеств повлияет на ZFC?
в ZF довольно легко доказать уникальность пустого множества так-то, прямо из самой первой аксиомы
CD
в ZF довольно легко доказать уникальность пустого множества так-то, прямо из самой первой аксиомы
вот её-то мы и выбрасываем, зачем она нужна :)
G
давайте тогда и все остальные выбросим
G
всё равно это уже будет не теория множеств, а теория именованных контейнеров
CD
в чем их принципиальные различия в конечном случае?
G
то есть, есть какие-то контейнеры, которые могут содержать какие-то элементы, в том числе и другие контейнеры. каждый контейнер уникален (имеет уникальный идентификатор), даже если элементы, которые он содержит, такие же, как у какого-нибудь другого
G
можно от этого попытаться определить пару, объединение, пересечение итд
CD
так в чем разница-то? определим рекурсивную равносоставленность и получим обычные конечные множества с другим значком
G
с парой проще всего, контейнер {A,B} это просто контейнер, в котором находятся контейнеры A и B
G
он только один
G
а вот объединение может быть разное
G
если определять AuB как контейнер, в котором есть все элементы, которые есть в A и в B, но может быть сколько угодно таких контейнеров с разными идентификаторами
G
он только один
кстати, нет, если у нас нет аксиомы эзистенциональности, у нас может быть сколько угодно контейнеров, содержащих эти два элемента
G
так в чем разница-то? определим рекурсивную равносоставленность и получим обычные конечные множества с другим значком
в общем, я готов дать ответ в чём разница. разница в том, что ни одно множество не уникально, так как равенство контейнеров определяется через равенство идентификаторов, а не элементов
CD
в общем, я готов дать ответ в чём разница. разница в том, что ни одно множество не уникально, так как равенство контейнеров определяется через равенство идентификаторов, а не элементов
всё так, и у нас есть некоторое свойство эквивалентности контейнеров, которое разведено с равенством, чтобы введенное ограничение аксиомы выбора на счетном множестве не смогло исчезать в дальнейших порождениях
G
ну то есть выходит та же ZF, только мы всегда говорим "эквивалентно" вместо "равно", ок



