Задания рассчитаны на 9-10 классы

​​#humor
Гений😉

​​#task
Пишите свой пример ответа в комментариях👇
...

​Два ребенка в дедушкином гараже собирают 2 велосипеда за 2 часа. Сколько понадобится детей, чтобы собрать 12 велосипедов за 6 часов?

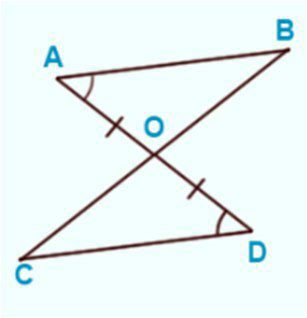
​​​По какому признаку треугольники AOB=DOС?

Вспомним сегодня с вами математику 6 класса

❗️Рациональные числа ❗️

Рациональные числа: определения, примеры


Данная статья посвящена изучению темы "Рациональные числа". Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет. 

Рациональные числа. Определения

Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой. 

Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.

Определение 1. Рациональные числа

Рациональные числа - числа, которые можно представить в виде положительной обыкновенной дроби [Math Processing Error]ab, отрицательной обыкновенной дроби [Math Processing Error]-ab или числа ноль. 

Таким образом, можно оставить ряд свойств рациональных чисел:

Любое натуральное число является рациональным числом. Очевидно, каждое натуральное число [Math Processing Error]n можно представить в виде дроби [Math Processing Error]1n.

Любое целое число, включая число [Math Processing Error]0, является рациональным числом. Действительно, любое целое положительное и целое отрицательное число легко представляется в виде соответственно положительной или отрицательной обыкновенной дроби. Например, [Math Processing Error]15=151, -352=-3521.

Любая положительная или отрицательная обыкновенная дробь [Math Processing Error]ab является рациональным числом. Это следует напрямую из данного выше определения.

Любое смешанное число является рациональным. Действительно, ведь смешанное число можно представить в виде обыкновенной неправильной дроби.

Любую конечную или периодическую десятичную дробь можно представить в виде обыкновенной дроби. Поэтому, каждая периодическая или конечная десятичная дробь является рациональным числом. 

Бесконечные и непериодическое десятичные дроби не являются рациональными числами. Их невозможно представить в форме обыкновенных дробей.

Приведем примеры рациональных чисел. Числа [Math Processing Error]5, 105, 358, 1100055 являются натуральными, положительными и целыми. Сдедовательно, это рациональные числа. Числа [Math Processing Error]-2, -358, -936 представляют собой целые отрицательные числа, и они также рациональны в соответствии с определением. Обыкновенные дроби [Math Processing Error]35, 87, -358 также являются примерами рациональных чисел.  

Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.

Определение 2. Рациональные числа

Рациональные числа - это такие числа, которые можно представить в виде дроби [Math Processing Error]±zn, где [Math Processing Error]z - целое число, [Math Processing Error]n - натуральное число.

Можно показать, что данное определение равносильно предыдущему определению рациональных чисел. Чтобы сделать это, вспомним, что черта дроби равносильна знаку деления. С учетом правил и свойств деления целых чисел, можно записать следующие справедливые неравенства:

[Math Processing Error]0n=0÷n=0; -mn=(-m)÷n=-mn.

Таким образом, можно записать:

[Math Processing Error]zn=zn, при z>00, при z=0-zn, при z<0

Собственно, данная запись и является доказательством. Приведем примеры рациональных чисел, основываясь на втором определении. Рассмотрим числа [Math Processing Error]-3, 0, 5, -755, 0,0125 и [Math Processing Error]-135. Все эти числа являются рациональными, так как  их можно записать в виде дроби с целым числителем и натуральным знаменателем: [Math Processing Error]-31, 01,-755, 12510000, 85.

Приведем еще одну эквивалентную форму определения рациональных чисел.

Определение 3. Рациональные числа

Рациональное число - это такое число, которое можно записать в виде конечной или бесконечной периодической десятичной дроби.

Данное определение напрямую следует из самого первого определения этого пункта. 

Подведем итог и сформулируем резюме по данному пункту:

Положительные и отрицательные дробные и целые числа составляют множество рациональных чисел.

Каждое рац

иональное число можно представить в виде обыкновенной дроби, числитель которой является целым числом, а знаменатель - натуральным числом.

Каждое рациональное число можно также представить в виде десятичной дроби: конечной или бесконечной периодической.

Слишком сложно?

Не парься, мы поможем разобраться и подарим скидку 10% на любую работу

Опиши задание

Какое из чисел является рациональным?

Как мы уже выяснили, любое натуральное число, целое число, правильная и неправильная обыкновенная дробь, периодическая и конечная десятичная дробь являются рациональными числами. Вооружившись этими знаниями можно без труда определить, является ли какое-то число рациональным.

Однако на практике часто приходится иметь дело не с числами, а с числовыми выражениями, которые содержат корни, степени и логарифмы. В некоторых случаях ответ на вопрос "рационально ли число?" является далеко не очевидным. Рассмотрим методы ответа на этот вопрос.

Если число задано в виде выражения, содержащего только рациональные числа и арифметические действия между ними, то результат выражения - рациональное число.

Например, значение выражения [Math Processing Error]2·318-0,250,(3) является рациональным числом и равно [Math Processing Error]18. 

Таким образом, упрощение сложного числового выражения позволяет определить, рационально ли заданное им число.

Теперь разберемся со знаком корня.

Оказывается, что число [Math Processing Error]mn, заданное в видя корня степени [Math Processing Error]n от числа [Math Processing Error]m рационально лишь тогда, когда [Math Processing Error]m является [Math Processing Error]n-ой степенью какого-то натурального числа.

Обратимся к примеру. Число [Math Processing Error]2 не является рациональным. Тогда как [Math Processing Error]9, 81 - рациональные числа. [Math Processing Error]9 и [Math Processing Error]81 - полные квадраты чисел [Math Processing Error]3 и [Math Processing Error]9 соответственно. Числа [Math Processing Error]199, 28, 151 не являются рациональными числами, так как числа под знаком корня не являются полными квадратами каких-либо натуральных чисел. 

Теперь возьмем более сложный случай. Является ли рациональным число [Math Processing Error]2435? Если возвести [Math Processing Error]3 в пятую степень, получается [Math Processing Error]243, поэтому исходное выражение можно переписать так: [Math Processing Error]2435=355=3. Следовательно, данное число рационально. Теперь возьмем число [Math Processing Error]1215. Это число нерационально, так как не существует натурального числа, возведение которого в пятую степень даст [Math Processing Error]121.

Для того, чтобы узнать, является ли логарифм какого-то числа [Math Processing Error]a по основанию [Math Processing Error]b рациональным числом необходимо применить метод от противного. К примеру, узнаем, рационально ли число [Math Processing Error]log25. Предположим, что данное число рационально. Если это так, то его можно записать в виде обыкновенной дроби [Math Processing Error]log25=mn.По свойствам логарифма и свойствам степени справедливы следующие равенства:

[Math Processing Error]5=2log25=2mn5n=2m

Очевидно, последнее равенство невозможно так как в левой и правой частях находятся соответственно нечетное и четное числа. Следовательно, сделанное предположение неверно, и число [Math Processing Error]log25 не является рациональным числом.

Стоит отметить, что при определении рациональности и иррациональности чисел не сторопостижных решений. Например, результат произведения иррациональных чисел не всегда является иррациональным числом. Наглядный пример: [Math Processing Error]2·2=2.

Также существуют иррациональные числа, возведение которых в иррациональную степень дает рациональное число. В степени вида [Math Processing Error]2log23 основание и показатель степени являются иррациональными числами. Однако само число является рациональным: [Math Processing Error]2log23=3.

​​#humor
ГЕНИАЛЬНО!!!

​​#task
Приносим извинения за долгое отсутствие и за не активность нашего администратора.
Команда "Пифагоры"
Канал будет действовать в новом постоянном режиме😊.
...
Трое друзей хотят купить книжку. Оказалось, что двоим на покупку книги не хватает 1 к., третьему 2р. 90к. Когда они сложили свои деньги, то денег на покупку книги им все равно не хватало. Зная, что денег у первого из друзей на 19 к. больше чем у второго, найдите, сколько денег было у каждого.


❗❗❗ ПОДСКАЗКА: у кого то денег может и не быть

#fact
Интересные математические факты 🤔
...
Интересные свойства числа 9 часто применяются в арифметике как для теоретических  
изысканий и практических действий, так и для составления различных занимательных задач  
или так называемых «головоломок».
Распространено также практическое применение девятки для проверки умножения и  
деления. Основано оно на том свойстве всякого числа, что остаток, получаемый от деления  
числа на девять, всегда равен остатку от деления на 9 суммы цифр этого числа. Укажем здесь  
еще несколько интересных применений этого числа.
Прежде всего нетрудно убедиться, что если мы напишем произвольное двузначное число, а  
затем напишем цифры этого же числа в обратном порядке и возьмем разность полученных  
чисел, то эта разность всегда разделится на 9.
Например,
72 − 27 = 45;
92 − 29 = 63;
63 − 36 = 27
и т. д.

Ребята, дети и взрослые ❗
Хорошие новости для всех на канале "Пифагоры"
Наша команда, хотела бы представь вам проект Popmath.
Сколько в нашем мире не нужной информации в интернете? Разве я не права? И в куче этого мусора, хотелось бы найти кое-что стоящее.
   
Для людей со всех уголков нашей Земли.
❗️Онлайн курсы❗️
Задачи и примеры с наивысшей степенью объяснения.
Умение читать и все. Остальному научит проект Popmath.

Онлайн курс даст понять тебе, насколько Математика прекрасна.

Высказывание Льва Толстого
"У меня есть целый мир знаний математических, естественных, языка и поэзии, передать которые у меня недостаёт времени"
Так и вы откройте для себя арифметический мир. Повышайте свой интеллект на карантине и становитесь умнее сидя дома 👌

Краткое описание курса Popmath и прочих условий по ссылке: http://popmath.ru/going_online/

Для остальных вопросов и записи в группу пишите @sowinaya_dusha

#task
Расставить скобки и знаки

Расставьте скобки и математические знаки так, чтобы равенство было верным:
9999999 = 100
Ответ найдете в комментариях👇

​​#humor
А кто ты?
Уже скоро...

​​#task
Объяснение с решением будет в нашей группе.
Задача "Трудный возраст"
...
Число исполнившихся мне в этом году лет во многом примечательно.
Если от этого числа отнять 2, то оно разделится на 3, а если от него отнять 3, то оно разделится на 2.
Если к нему прибавить 4, то оно разделится на 5, а если от него отнять 5, то оно разделится на 4.
Если от него отнять 5, то оно разделится на 6, а если от него отнять 6, то оно разделится на 5.
Если к нему прибавить 7, то оно разделится на 8, а если к нему прибавить 8, то оно разделится на 7.
 Сколько же лет мне исполнилось в этом году?
Пиши ответы в комментариях 👇

#humor
Ничего лишнего😂
Просто посмотрите