А скажите, в любом топосе power object задаёт функтор?

Ага. По определению — это стрелки в омегу.
Ну точнее, экспоненциальный объект, ну там видно.

https://ncatlab.org/nlab/show/power+object
Let C be a category with finite limits.
A power object of an object c∈C is
an object Ω^c
a monomorphism ∈c → c×Ωc

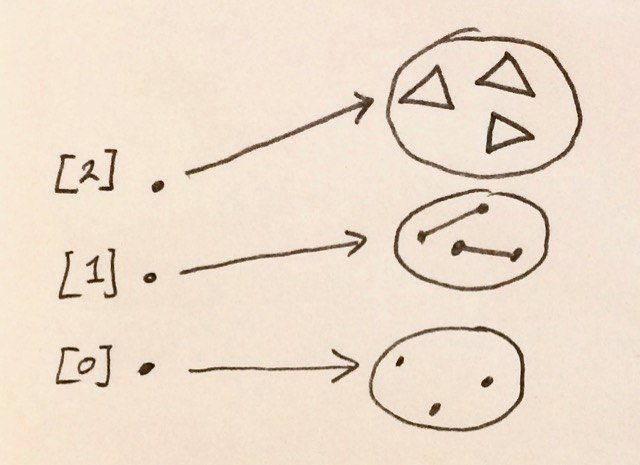
На первый взгляд, неплохое введение в тему "про симплициальное" —
https://bartoszmilewski.com/2018/12/11/keep-it-simplex-stupid/
#link #paper

ну это получается контрвариантный.
А ковариантный ?

Ну если он по определению такой, что уж тут поделаешь? ;-)
Может быть, какой-то ковариантный функтор канонiчно строится по power object'у...
Это имеется в виду?

да, аналогичный ковариантному poser set functor как здесь например https://proofwiki.org/wiki/Definition:Power_Set_Functor

Ну вот, два хороших функтора ;-)

первый можно построить для любого топоса (я просто едва понимаю, что такое топос)

Для любой регулярной категории...

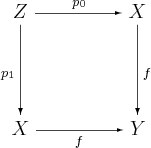
Во втором нужны pullback'и.

Опять регулярные категории. Я сегодня уже не справился с их определением когда читал статью фонга из моноидального

Нуууу
https://ncatlab.org/nlab/show/regular+category
https://en.wikipedia.org/wiki/Regular_category

Ещё про пучко-топосы я лично рекомендую книжку Маклейна-Мёрдока.
На мой взгляд, она лучшая. И лишнего почти нет.

На мой взгляд, для начала, невредно понять следующий частный случай — топос предпучков топосов.
И в частности, топос предпучков множеств.
Очень во многом, можно сказать, что понятие топоса, это лёгкое обобщение категории предпучков достаточно хороших категорий (например, множеств).
И можно начинать изучать пучко-топосы конкретно так с изучения категории предпучков C→Set.
Это важный частный случай, на котором можно продемонстрировать прям всё-всё топосное.

А если с претопосами связываться, то без регулярных уже никак ;-)
И без чОтких (coherent) тоже никак :-)

Можно ли на примере Maybe(Option) объяснить как монада является моноид в категории эндофункторов ?

Напишите умножение монады и её единицу.
Это более правильное определение, чем через bind.
Умножение: Maybe (Maybe x) → Maybe x
Единица: x → Maybe x
И покажите, что удовлетворяет монадным законам.
Для начала, разверните в "программистский вид" классическое определение —
https://en.wikipedia.org/wiki/Monad_(category_theory)
Вот именно это мю и есть умножение в моноиде в (строгой моноидальной) категории эндофункторов.

Совершенно точно, что стоит посмотреть на монады со стороны именно монадного умножения, а не bind.
Это более общее определение и эквивалентно "программистскому" оно только для категорий специального вида (какой является, например, Hask).
Ну и в целом, такое определение совершенно точно позволит лучше понимать, что такое монада.
Потом, можно посмотреть на моноидальные категории (может быть, для начала, какого-то более простого вида, типа симметричных или вообще строгих) и определение моноида в моноидальной категории.
Потом увидеть, что определение монады, это оно и есть, только в качестве моноидального произведения выступает композиция функторов.
Потом разобрать понятие алгебры для монады.
Оно интересное даже в чисто программистском смысле даже на таких функторах, как Maybe.
И обязательно примеры.
Категории алгебр тоже, наверное, будут любопытными...