VY
Тогда для любой пары f: A-> Int, g : A-> String, мы всё ещё можем найти fxg: A -> X, но не единственным образом, мы можем взять
a => (f(a), g(a), true) либо a => (f(a), g(a), false)
Size: a a a
VY
SK
к
Oℕ
Oℕ
Oℕ
λ
NI
IJ
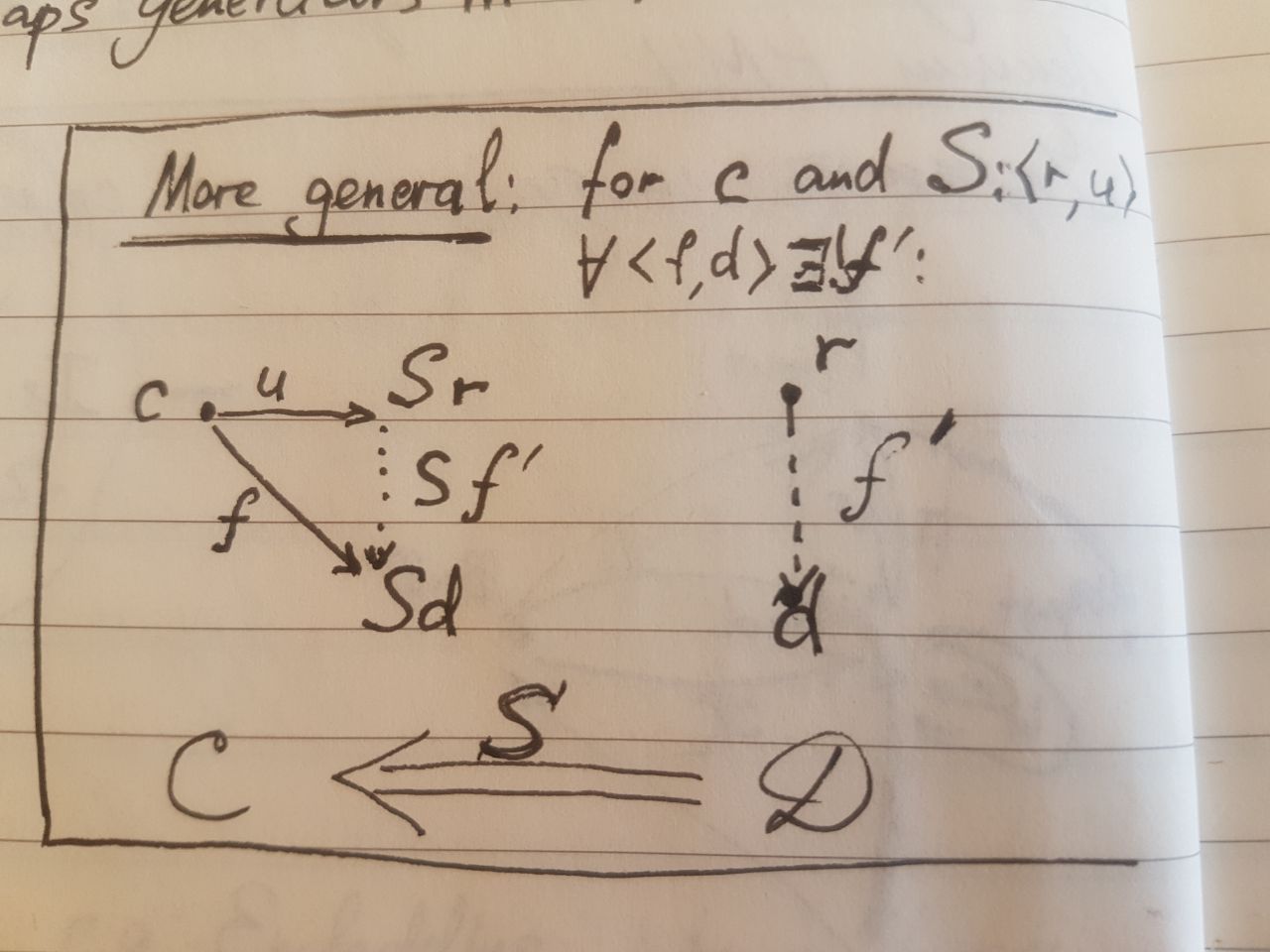
(u,r) универсальная стрелка для функтора S:D->C и объекта c \in C если любой морфизм из c в кодомен S можно выразить единственным образом через композицию с u. С точки зрения умозрительного построения путей получается, что u как бы универсальная точка входа, и любоф другой путь в кодомен S можно пропустить через u.IJ
IJ
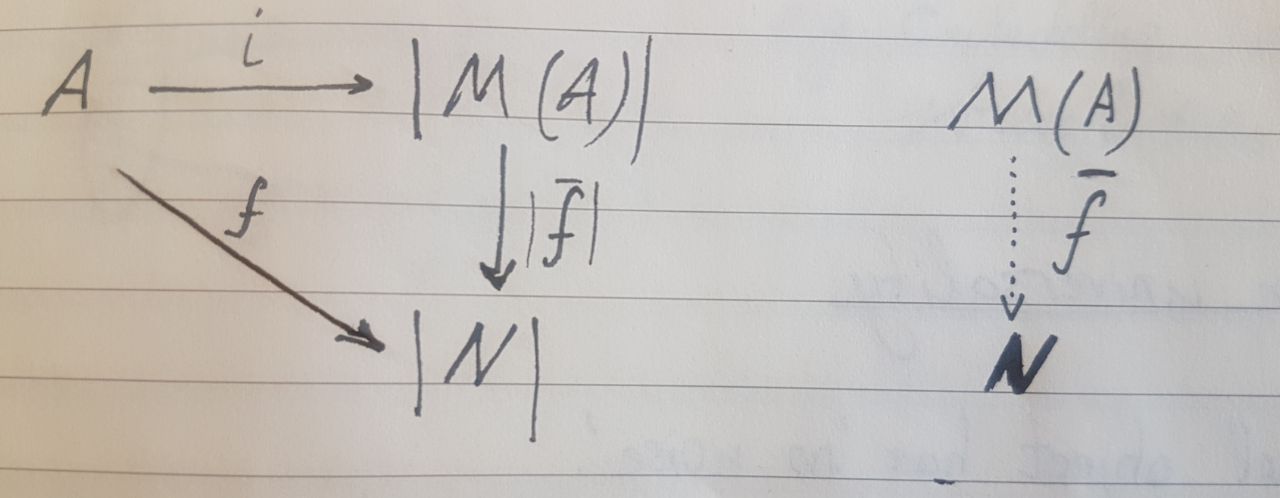
IJ
SK
Oℕ
NI
IJ
SK
IJ
NI
IJ