NI
Этточно.
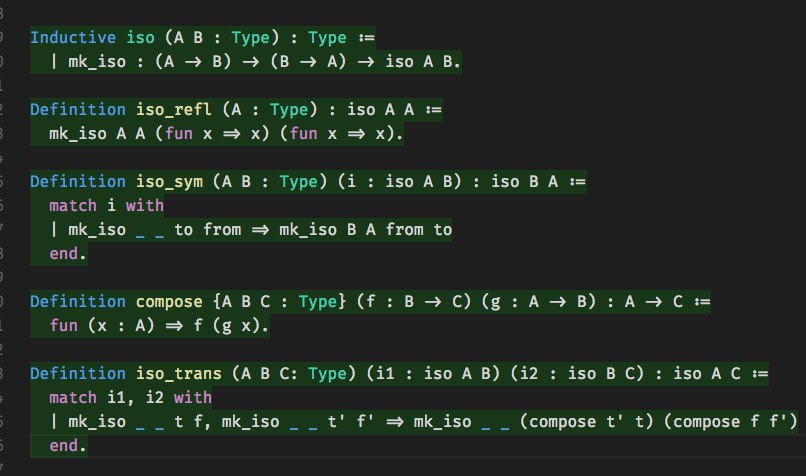
наверное это можно считать решением, хоть это не пруф вовсе
а то я чет хз как доказывать такие вещи, и уж тем более на бумаге
описывать категории что ли
Size: a a a
2018 April 06
PG
кстати, тут необязательно делать индуктивный тип, можно просто:
Definition iso (A B : Type) : Type := (A \to B) * (B \to A).
P
Ну не на бумаге же доказывать
лол
DM
подскажите такой момент, в лекциях Бартоша и на вики https://en.wikipedia.org/wiki/Representable_functor representable functor определен на ковариантном хом-функторе
а в https://ncatlab.org/nlab/show/representable+functor определен на контравариантном
кому верить? или это верно для всех вариативностей?
а в https://ncatlab.org/nlab/show/representable+functor определен на контравариантном
кому верить? или это верно для всех вариативностей?
AG
дак там хомы разные
AG
в википедии Hom(A,–), а на нкате hom C(−,X)
PG
Это оно?
Oℕ
дак там хомы разные
ну так там и разница, что в одном месте
C → Set, а в другом C op→Set
C → Set, а в другом C op→Set
AG
дыа
Oℕ
но мне кажется, что эти определения +- эквивалентные
Oℕ
Но типа какое из них каноничнее-таки
Oℕ
Для ковариантных, контравариантых, или оба?
AG
ну на нкате они это для пучков делают, которые контравариантные
AG
а на вики более отдельное определение
AG
там есть упоминание в definition
NI
Для ковариантных, контравариантых, или оба?
Оба нужны.
Ну и ещё, рассматривают функторы вида C^op x C → Set
Hom от двух параметров именно такой, ну и "самый канонiчный" из таких ;-)
Ну и ещё, рассматривают функторы вида C^op x C → Set
Hom от двух параметров именно такой, ну и "самый канонiчный" из таких ;-)
DM
Оба нужны.
Ну и ещё, рассматривают функторы вида C^op x C → Set
Hom от двух параметров именно такой, ну и "самый канонiчный" из таких ;-)
Ну и ещё, рассматривают функторы вида C^op x C → Set
Hom от двух параметров именно такой, ну и "самый канонiчный" из таких ;-)
т.е. "представляющий" функтор можно и на ко- и на контрвариантном задавать?
AG
почему бы и нет, просто изоморфизм с другим хомяком как я понимаю
KV
Эта ваша эдукера очень странно себя ведёт