Size: a a a
2017 February 05
2017 February 06

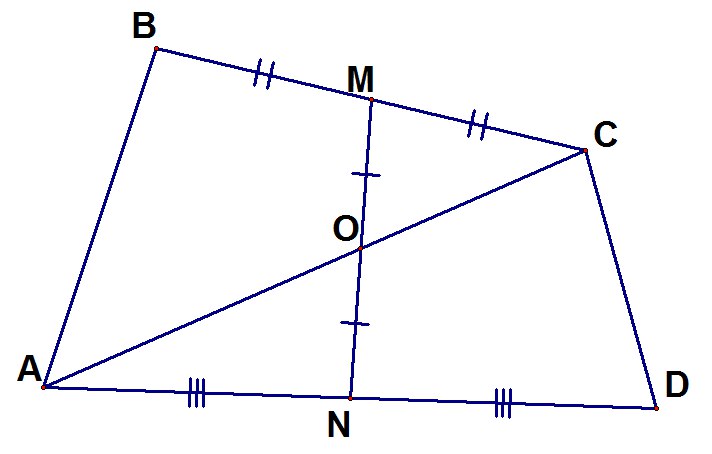
23. В выпуклом четырёхугольнике ABCD отмечены середины противоположных сторон BC и AD – точки M и N. Диагональ AC проходит через середину отрезка MN. Найдите площадь АВСD, если площадь треугольника АВС равна S.
2017 February 07

Задачу 23 можно решать многими способами. Вот один из них:

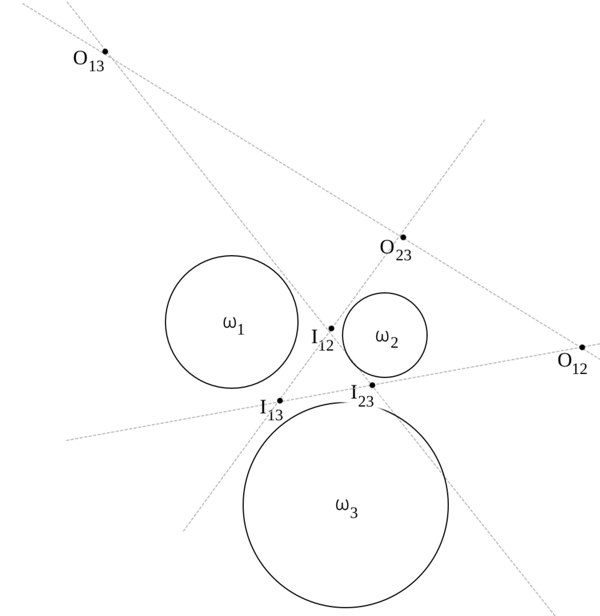
24. В треугольник АВС вписана окружность. Из середины каждого отрезка, соединяющего
две точки касания, проводится перпендикуляр к противолежащей стороне. Докажите, что
эти перпендикуляры пересекаются в одной точке.
две точки касания, проводится перпендикуляр к противолежащей стороне. Докажите, что
эти перпендикуляры пересекаются в одной точке.

Не поленилась и написала несколько разных способов решить задачу 23: http://telegra.ph/Reshenie-zadachi-23-02-07

Решение задачи 24
2017 February 08

25. Параллелограмм и квадрат расположены так, что вершины квадрата лежат на сторонах параллелограмма (по одной вершине на каждой стороне). Из каждой вершины параллелограмма проведена прямая перпендикулярная ближайшей стороне квадрата. Докажите, что точки попарного пересечения этих прямых также являются вершинами квадрата.

Решение задачи 25
2017 February 09

26. Существует ли многогранник, проекциями которого на три попарно перпендикулярные плоскости являются: треугольник, четырехугольник и пятиугольник?

Решение «еженедельного гроба», задачи 20:
http://telegra.ph/Reshenie-Zadachi-20-02-09
http://telegra.ph/Reshenie-Zadachi-20-02-09
2017 February 10

Решение задачи 26:
Конечно, существует. Таких многогранников много. Приведу два примера, которые получаются вырезанием кусочков из прямой треугольной призмы:
Конечно, существует. Таких многогранников много. Приведу два примера, которые получаются вырезанием кусочков из прямой треугольной призмы:

27. В некоторый момент угол между часовой и минутной стрелками равен α. Через час он опять равен α. Найдите все возможные значения α.

Решение задачи 27.
2017 February 12

Каналу месяц. За это время пришли 530 подписчиков, авторов стало больше, я научилась прятать решения. Спасибо всем вам за то, что решаете задачки. Если вам нравится, поделитесь ссылкой со своими друзьями, пусть они тоже встречаются с геометрией каждый день: t.me/geometrykanal

Костя Кноп нашел источник книг Григория Филипповского по геометрии. Там не только геометрия, а еще и о слоненке есть: http://zadacha.uanet.biz/home/druzja-i-ikh-raboty/filippovskij-g/matematika
2017 February 13

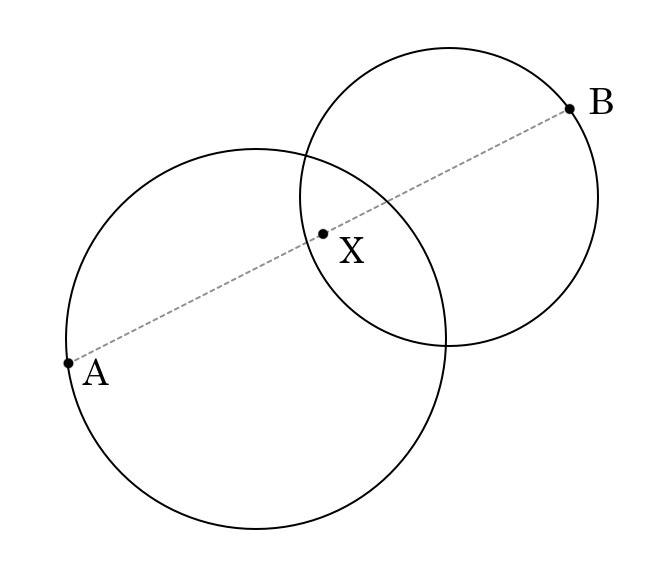
28. На гипотенузе AB прямоугольного треугольника ABC выбрана такая точка D, что BD = BC, а на катете BC — такая точка E, что DE = BE. Докажите, что AD + CE = DE.
2017 February 14

Решение задачи 28.