Size: a a a
2019 December 02
2019 December 03

331. Вписанная окружность треугольника АВС касается стороны АС в точке D. Вторая окружность проходит через точку D, касается луча ВА в точке А и, кроме того, касается луча ВС. Найдите отношение АD : DC.
#задача
#задача
2019 December 06

http://geometry.ru/olimp/2020/zaoch.pdf
http://geometry.ru/olimp/2020/zaoch_eng.pdf
начался заочный тур XVI геометрической олимпиады им. Шарыгина (24 задачи для разных классов, в основном непростые)
http://geometry.ru/olimp/2020/zaoch_eng.pdf
начался заочный тур XVI геометрической олимпиады им. Шарыгина (24 задачи для разных классов, в основном непростые)

332. Ортоцентр H треугольника ABC лежит на вписанной в треугольник окружности.
Докажите, что три окружности с центрами A, B, C, проходящие через H, имеют общую касательную.
#задача
Докажите, что три окружности с центрами A, B, C, проходящие через H, имеют общую касательную.
#задача
2019 December 07

Переслано от Наталья Нетрусова...
Видеозаписи спецкурса по геометрии 8 класса, ведущий Ю.А. Блинков.
На сайте школы Летово еженедельно выкладываются материалы спецкурса по геометрии, который изучают их школьники: короткий ролик на 8-12 минут и листок со всеми задачами. Сейчас выложено 8 занятий.
Первый ролик выложен в свободный доступ: https://letovo.ru/obrazovanie/vebinars/
Остальные материалы доступны тем, кто зарегистрировался как поступающий. Эта регистрация, конечно, ни к чему не обязывает. Нужно зайти на страницу и выбрать там углубленную математику: https://letovo.ru/postuplenie/rekomendatsii-po-podgotovke-k-testirovaniyu/
На сайте школы Летово еженедельно выкладываются материалы спецкурса по геометрии, который изучают их школьники: короткий ролик на 8-12 минут и листок со всеми задачами. Сейчас выложено 8 занятий.
Первый ролик выложен в свободный доступ: https://letovo.ru/obrazovanie/vebinars/
Остальные материалы доступны тем, кто зарегистрировался как поступающий. Эта регистрация, конечно, ни к чему не обязывает. Нужно зайти на страницу и выбрать там углубленную математику: https://letovo.ru/postuplenie/rekomendatsii-po-podgotovke-k-testirovaniyu/
2019 December 08

https://www.geogebra.org/m/kyudvqfx
А.И.Сгибнев сделал альбом подвижных чертежей (уже больше 130) к задачнику М.А.Волчкевича. Можно пользоваться, копировать, показывать на уроке и т.д.
А.И.Сгибнев сделал альбом подвижных чертежей (уже больше 130) к задачнику М.А.Волчкевича. Можно пользоваться, копировать, показывать на уроке и т.д.
2019 December 09

2019 December 10

Переслано от Наталья Нетрусова...
В четверг (12.12) на семинаре учителей математики Д.Швецов расскажет об опыте использования книг из серии «Математические кружки», а Н.Наконечный — про задачи о турнирах.
Как водится, с 19:00, в столовой МЦНМО на 1 этаже, приглашаются все желающие.
https://mccme.ru/nir/seminar/ #mccme_tseminar
Как водится, с 19:00, в столовой МЦНМО на 1 этаже, приглашаются все желающие.
https://mccme.ru/nir/seminar/ #mccme_tseminar
2019 December 11

333. В треугольнике ABC прямые, на которых лежат медиана BK и биссектриса BE, делят высоту AD на три равных части. Найти AC если AB = 4.
#задача
#задача
2019 December 13

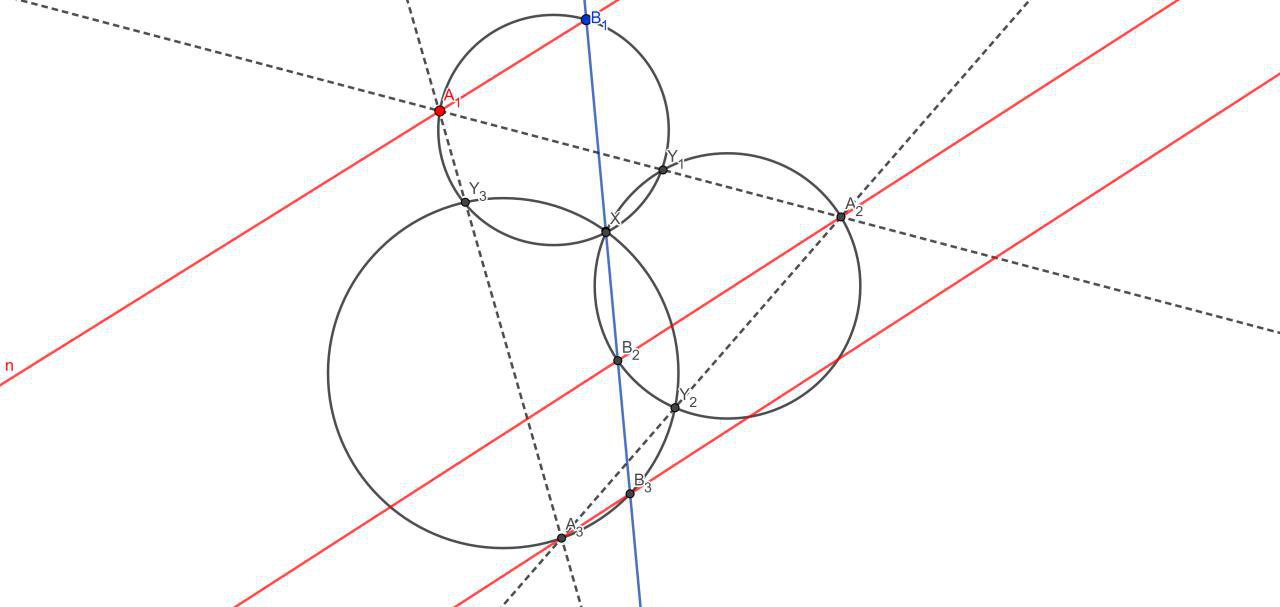
Немного про перекидывание точек с окружности на окружность
(факты без доказательств — если не знаете, докажите сами)
1) Две окружности пересекаются в точках X, Y, и точки A, B лежат на первой окружности. Обозначим A1, B1 точки пересечения прямых AX, BY соответственно со второй окружностью. (Дальше будем для краткости говорить «перебросили точки A и B через точки X и Y») Тогда A1B1 параллельно AB.
2) Три окружности проходят через одну точку X, а их вторые точки пересечения называются Y1, Y2, Y3. На одной из окружностей взяли точку A1 и последовательно перебросили через точки Y1, Y2, Y3. Тогда результатом последнего перебрасывания снова будет точка A1 — или, что то же самое, A1, A3 и Y3 лежат на одной прямой.
3) А если в условии пункта 2) окружности не проходят все через одну точку? Утверждается, что тогда после трёх перебрасываний мы точно не получим исходную точку. Не верите? Проверьте сами, а потом и докажите.
4) Скомбинируем пункты 1) и 2) — добавим точку B1 на той же окружности, что и A1, но её будем
(факты без доказательств — если не знаете, докажите сами)
1) Две окружности пересекаются в точках X, Y, и точки A, B лежат на первой окружности. Обозначим A1, B1 точки пересечения прямых AX, BY соответственно со второй окружностью. (Дальше будем для краткости говорить «перебросили точки A и B через точки X и Y») Тогда A1B1 параллельно AB.
2) Три окружности проходят через одну точку X, а их вторые точки пересечения называются Y1, Y2, Y3. На одной из окружностей взяли точку A1 и последовательно перебросили через точки Y1, Y2, Y3. Тогда результатом последнего перебрасывания снова будет точка A1 — или, что то же самое, A1, A3 и Y3 лежат на одной прямой.
3) А если в условии пункта 2) окружности не проходят все через одну точку? Утверждается, что тогда после трёх перебрасываний мы точно не получим исходную точку. Не верите? Проверьте сами, а потом и докажите.
4) Скомбинируем пункты 1) и 2) — добавим точку B1 на той же окружности, что и A1, но её будем

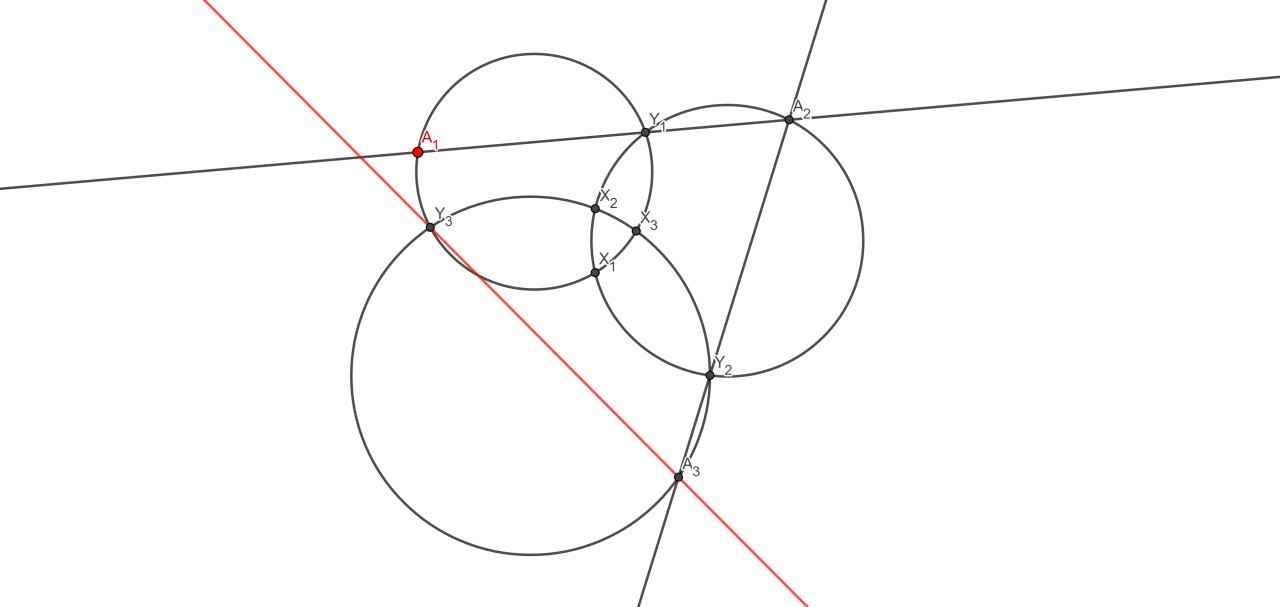
перебрасывать через X. Конечно же, все три точки лягут на одну прямую — и прямые A1B1, A2B2, A3B3 будут параллельны.
Пункты 1) и 2) легко обобщаются на случай любого числа окружностей. И если в пункте 1) эти окружности вовсе не обязаны проходить через одну точку, то в пункте 2) это становится необходимым условием, если не менять формулировку задачи.
А что если, в случае трёх окружностей, не проходящих через одну точку, перебрасывать через все шесть точек пересечения? Вдруг получится что-то интересное?
Пункты 1) и 2) легко обобщаются на случай любого числа окружностей. И если в пункте 1) эти окружности вовсе не обязаны проходить через одну точку, то в пункте 2) это становится необходимым условием, если не менять формулировку задачи.
А что если, в случае трёх окружностей, не проходящих через одну точку, перебрасывать через все шесть точек пересечения? Вдруг получится что-то интересное?

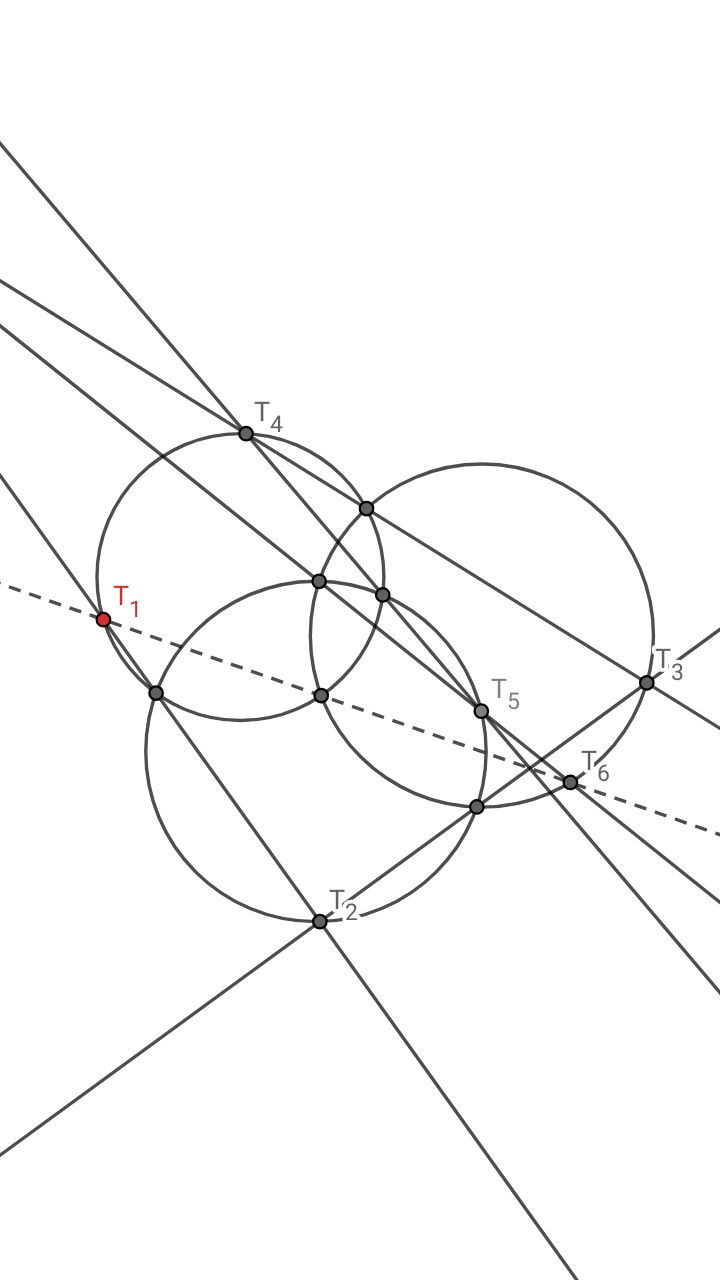
А вот и картинка для случая трёх окружностей, не проходящих через одну точку. Цепь перебрасываний снова замкнется, причем порядок можно выбирать по-разному (как?)
Если вы не знали об этом — докажите с:
А как обобщить конструкцию на случай n окружностей?
Если вы не знали об этом — докажите с:
А как обобщить конструкцию на случай n окружностей?

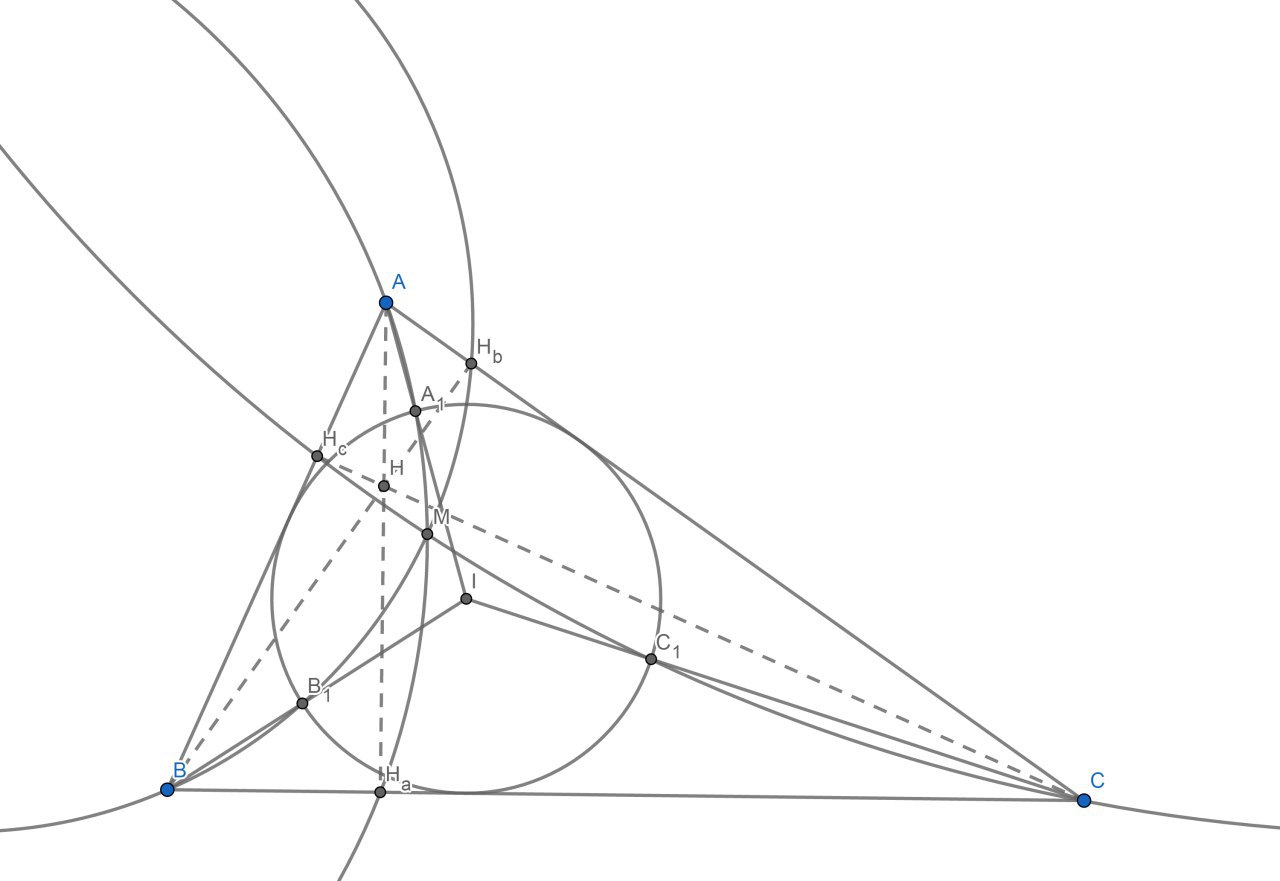
Немного отвлечёмся от вышеописанного сюжета, хотя дальше речь тоже пойдёт про три окружности.
Далее будем говорить, что «три окружности пересекаются в двух точках», если существуют две различные точки на плоскости, через которые проходит любая из данных трёх окружностей.
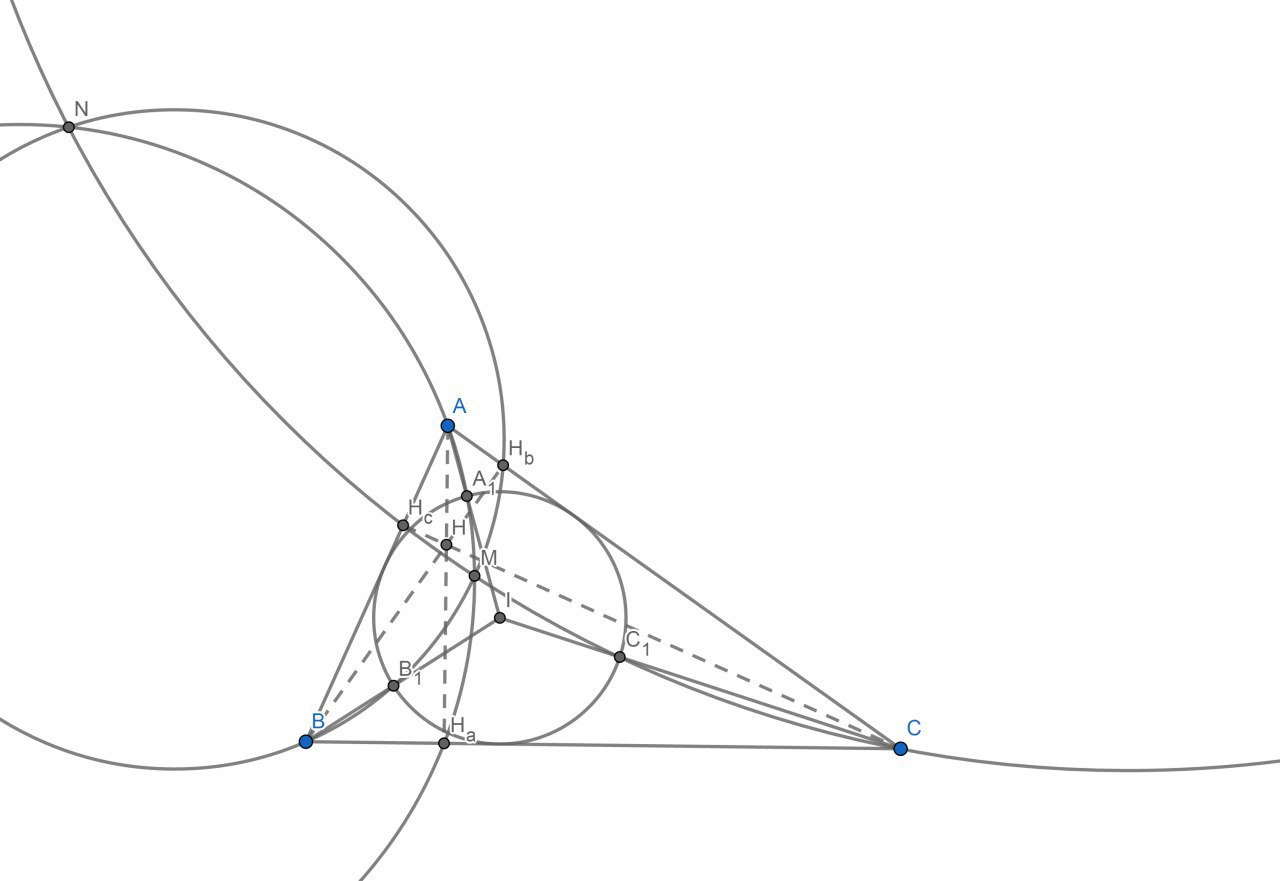
Итак, пусть у нас есть треугольник ABC, в который вписана окружность ω с центром I. A_1 = AI ∩ ω. H_a — проекция A на BC. Опишем окружность Ω_a около треугольника AH_aA_1. Окружности Ω_c и Ω_b определяются аналогично. Тогда оказывается, что три окружности, определенные таким образом, либо не имеют общих точек, либо касаются, либо пересекаются в двух точках.
Далее будем говорить, что «три окружности пересекаются в двух точках», если существуют две различные точки на плоскости, через которые проходит любая из данных трёх окружностей.
Итак, пусть у нас есть треугольник ABC, в который вписана окружность ω с центром I. A_1 = AI ∩ ω. H_a — проекция A на BC. Опишем окружность Ω_a около треугольника AH_aA_1. Окружности Ω_c и Ω_b определяются аналогично. Тогда оказывается, что три окружности, определенные таким образом, либо не имеют общих точек, либо касаются, либо пересекаются в двух точках.

Возможно три типа треугольника ABC:
1) тупоугольный — окружности не пересекаются
2) остроугольный — окружности пересекаются в двух точках
3) прямоугольный — окружности также пересекаются в двух точках, причём одна из них совпадает с вершиной прямого угла
Отметим, что иногда данные три окружности могут касаться, и две точки их пересечения могут вырождаться в одну. Интересно, когда так происходит?
1) тупоугольный — окружности не пересекаются
2) остроугольный — окружности пересекаются в двух точках
3) прямоугольный — окружности также пересекаются в двух точках, причём одна из них совпадает с вершиной прямого угла
Отметим, что иногда данные три окружности могут касаться, и две точки их пересечения могут вырождаться в одну. Интересно, когда так происходит?
2019 December 16

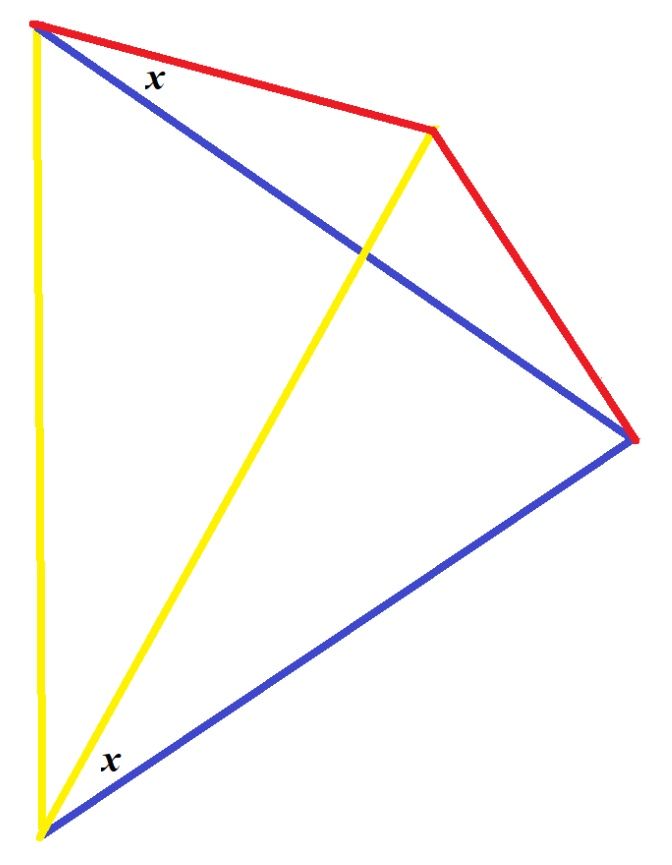
334. В этой задаче не дано ни одного численного значения.
Отрезки одного цвета одной длины. Найти угол х.
Задачка из твиттера Philip Gibbs #задача
Отрезки одного цвета одной длины. Найти угол х.
Задачка из твиттера Philip Gibbs #задача
2019 December 21

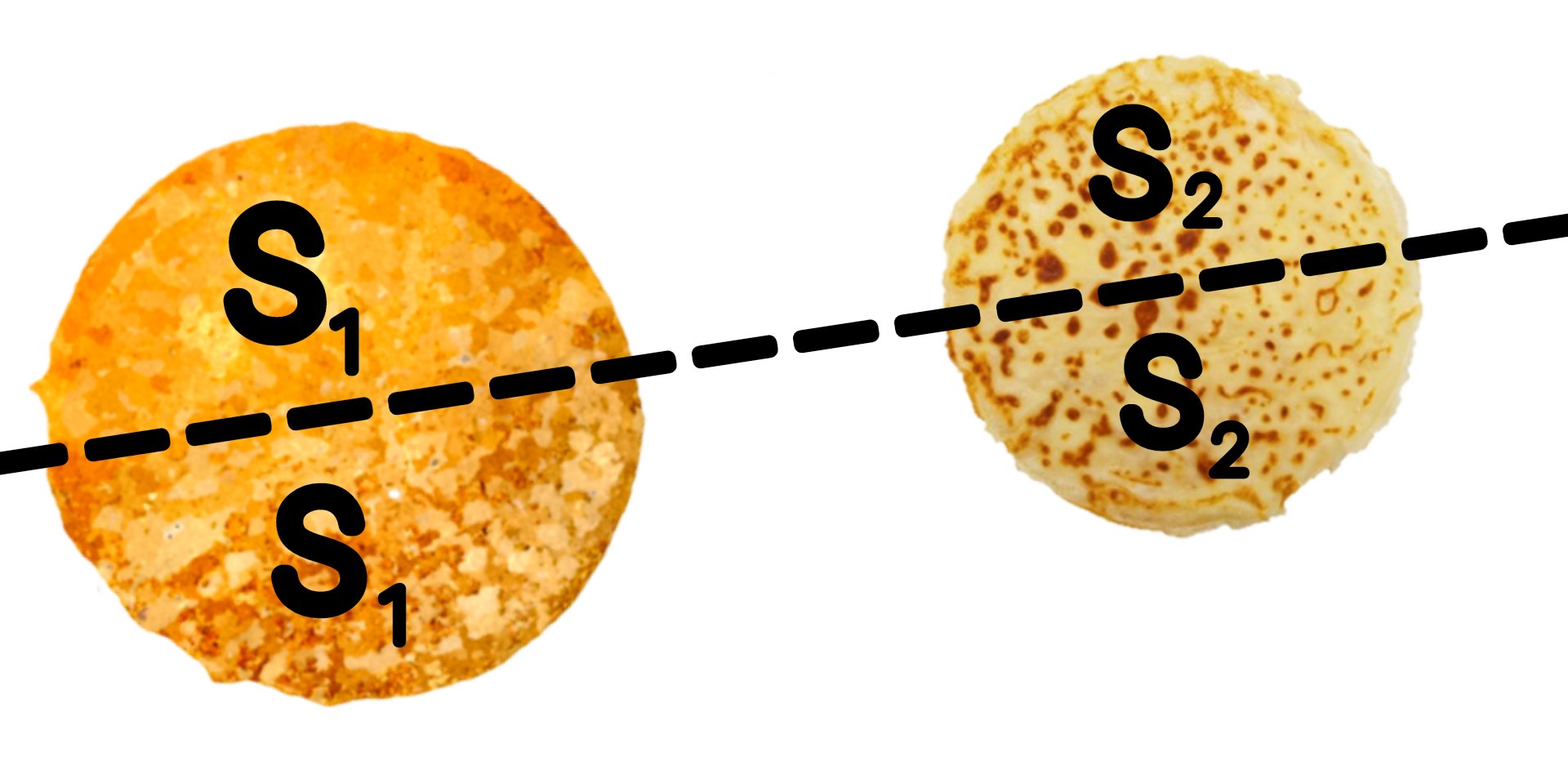
Теорема о блинах🥞
Теорема утверждает, что любые два блина (считаем их плоскими) всегда можно разрезать одним движением ножа так, чтобы каждый из них был разделен на две равные по площади части.
Другими словами через любые две фигуры лежащие в одной плоскости можно провести прямую так, чтобы она делила каждую из фигур на две равновеликие (равные по площади) фигуры.
Теорема утверждает, что любые два блина (считаем их плоскими) всегда можно разрезать одним движением ножа так, чтобы каждый из них был разделен на две равные по площади части.
Другими словами через любые две фигуры лежащие в одной плоскости можно провести прямую так, чтобы она делила каждую из фигур на две равновеликие (равные по площади) фигуры.
2019 December 24
2019 December 26

https://mccme.ru/head/zmk.html
по ссылке теперь собраны разные заочные мат. конкурсы, которые сейчас бывают — в них могут найти себе интересные и осмысленные задачи и 7-классники, и младшекурсники
по ссылке теперь собраны разные заочные мат. конкурсы, которые сейчас бывают — в них могут найти себе интересные и осмысленные задачи и 7-классники, и младшекурсники