Подобным образом замощения помогают решить разные задачи на разрезание. Например, при помощи такого замощения квадратами можно доказать теорему Пифагора.

Видеозапись лекции Г.Б. Филипповского

Григорий Борисович Филипповский прочитал в школе «Летово» лекцию для учителей математики, посвящённую недавним находкам учеников на уроках геометрии.
 
Видеозапись: https://www.youtube.com/watch?v=zB99ZrqOQsU&feature=emb_logo

в этот четверг (13.02) в МЦНМО на семинаре учителей математики

А.И.Сгибнев будет показывать свой альбом подвижных чертежей к книге М.А.Волчкевича и рассказывать про возможности программ динамической математики,

И.В.Раскина будет рассказывать про их с А.В.Шаповалов новую книгу «Комбинаторика для начинающих» (из серии «Школьные математические кружки»)

https://mccme.ru/nir/seminar/

Лекторий РЦ 57

Ближайшая лекция пройдет 19 февраля с 16:30 до 18:30 в школе № 57.
Тема: «Интересные задачи по геометрии».
Докладчик: Рафаил Калманович Гордин

Подробности и регистрация: https://vertical.sch-int.ru/lektorij-rc-57-4/

В связи в этой лекцией не вредно напомнить про информационно-поисковую систему «Задачи по геометрии»: http://zadachi.mccme.ru/

Вдруг кто не видел еще.

10 доказательств того, что высоты пересекаются в одной точке

Может кто-нибудь знает еще? Пишите в чат

Смотрите какой еще канал есть:

Позавчера закончился Уральский турнир. Смотрите список всех геометрических задач. Особенно интересная задача 4 из финала высшей лиги.

https://zen.me/Nlm4I

напомним, что заочный тур геометрической  олимпиады им. Шарыгина заканчивается в это воскресенье, 1 марта

Существует ли тетраэдр, в сечениях которого двумя разными плоскостями получаются квадраты 1×1 и 100×100?

// задача М.Евдокимова на ММО сегодня, https://mccme.ru/mmo/2020/

появились решения заочного тура олимпиады им. Шарыгина

http://geometry.ru/olimp/2020/zaoch_sol.pdf

339. (Японская теорема) Дан вписанный четырехугольник ABCD.
а) Докажите, что центры вписанных окружностей треугольников ABC, BCD, CDA, DAB образуют прямоугольник.
б) Отметим теперь для каждого треугольника центры не только вписанных, но и вневписанных окружностей. В какую фигуру складываются все 16 центров?

#задача

Методическое объединение ШАГ

Методическое объединение ШАГ —  группа учителей, которые делятся своим опытом работы в школе.

В своем канале в Телеграме, в группах в VK и Facebook они предлагают приемы для уроков, рассказывают о полезных книгах и видео.

ТГ: @shagtelegram
ВК: https://vk.com/shag.education
ФБ: https://www.facebook.com/groups/shag.education/

Кроме того, ШАГ проводит вебинары и семинары для учителей: http://shag.education/

Недавно мне встретилась известная конструкция и я захотел поделиться ею с вами. Тем, кому она уже знакома, думаю, будет не лишним вспомнить, а тем, кто ни разу с ней не встречался, полезно узнать.

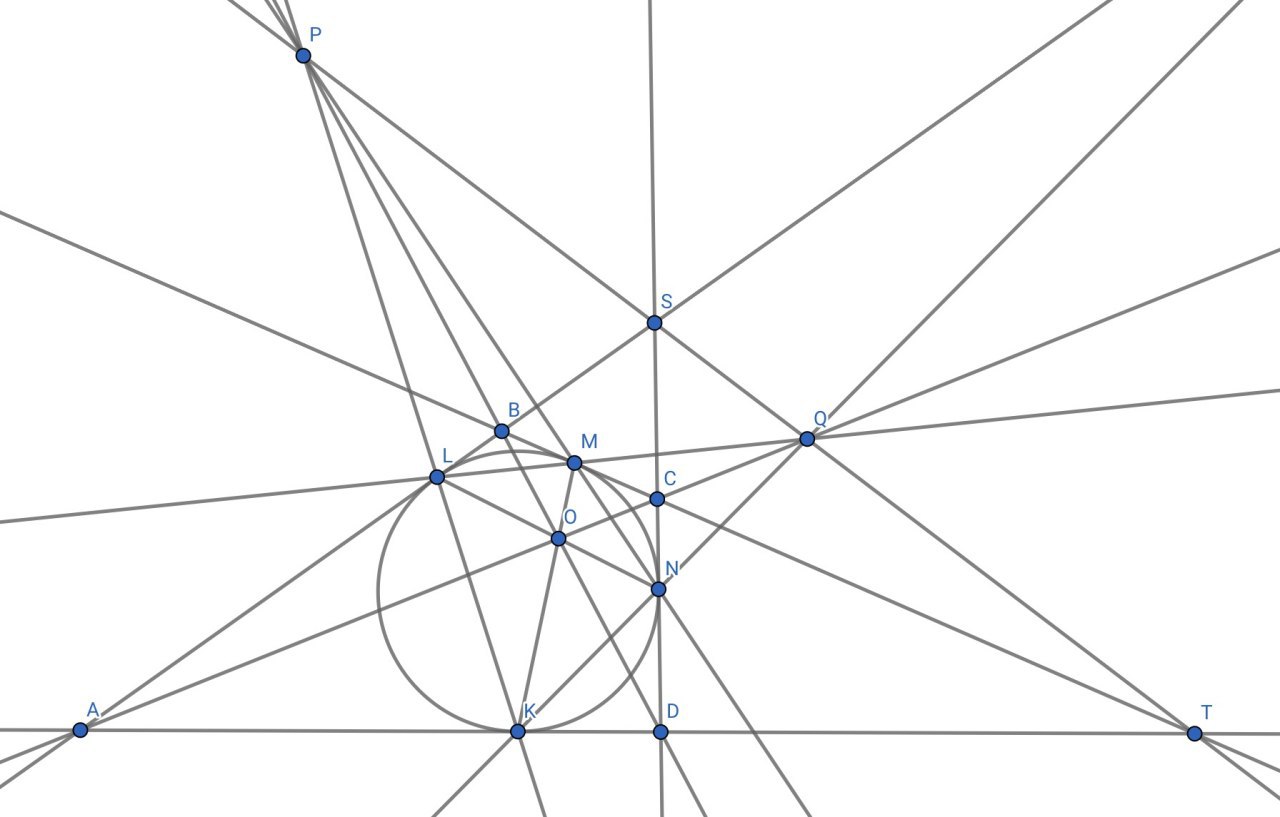
Итак, приступим. Дан описанный четырёхугольник ABCD, вписанная окружность которого касается сторон DA, AB, BC, CD в точках K,L,M,N соответственно. Пусть S = AB∩CD и T = BC∩AD. Тогда

1) прямые AC, BD, KM, LN пересекаются в точке O
2) прямые MN, KL, BD пересекаются в точке P
2*) аналогично прямые LM, KN, AC пересекаются в точке Q
3) P,S,Q,T лежат на одной прямой (подсказка: подумайте, как это соотносится с 1 пунктом)
4) (P,Q;S,T)=-1

P.S. Думаю, что это очевидно, но всё же упомяну, что никакого счёта тут не требуется. (так как я видел некоторые счётные доказательства вышеприведённых фактов)

https://zen.me/1AXfxZ Отправлено из Yandex Zen

Задачка дня (голову ломал целый день). Много чего наковырял там (окружность 9 точек, симметрии, много вписанных углов), но мало что пригодилось. Есть ощущение, что всё ещё проще, но...
Дерзайте!

340.

(вариация теоремы о бабочке)

Через точку A, не лежащую на окружности, проведены две прямые, пересекающие эту окружность, одна – в точках P1, P2, другая – в точках Q1, Q2 . Произвольная прямая, проходящая через A, пересекает окружность в точках M1, M2 , а описанные окружности треугольников AP1Q1 и AP2Q2 – в точках N1 и N2 соответственно. Тогда M1N1 = M2N2 .

#задача