https://klarissa45.livejournal.com/188617.html

про детские (с интересных дошкольникам начиная) книжки, связанные с математикой

Откровенно лженаучная и псевдоисторическая "Новая хронология" Анатолия Фоменко вызвала, тем не менее, бурные дискусии и профессиональный разбор в научной среде во многом из-за того, что автор — большой ученый в другой области. Выдающийся математик, академик РАН.

Заслуги Анатолия Тимофеевича в математике настолько бесспорны, что выдающийся лингвист, академик Андрей Зализняк какое-то время думал, что Фоменко просто шутит.

"Признаюсь, я сам не могу до конца отделаться от мысли, что для А.Т.Ф. его сочинения на гуманитарные темы — это забавный, хотя и изрядно затянутый фарс, мефистофелевская насмешка математика над простофилями гуманитариями, наука которых настолько беспомощна, что они не в состоянии отличить пародию от научной теории" ( http://www.mathnet.ru/links/250e6c2130d0e7634b0e2ab8c66d8485/rm288.pdf )

Далее Зализняк без особого труда разбивает "сенсационные" утверждения Фоменко вроде того, что река Темза это на самом деле пролив Босфор. Но его статья даже более интересна мыслями о соотношении наук, которые он высказывает по ходу развенчивания "Новой хронологии".

Что с того, что Фоменко большой математик? Собственно математики-то в "Новой хронологии" и нет — там не выводятся формулы и не доказываются теоремы. А если автор начинает проводить статистический анализ времён правления царей, так он должен сначала изучить времена этих царей как заправский историк. То же касается лингвистических и географических "открытий" Фоменко.

Не будем пересказывать всю статью, лучше почитайте оригинал.  Академик Зализняк был большим знатоком  языка и писал безупречно — и литературно, и логически
@obznam

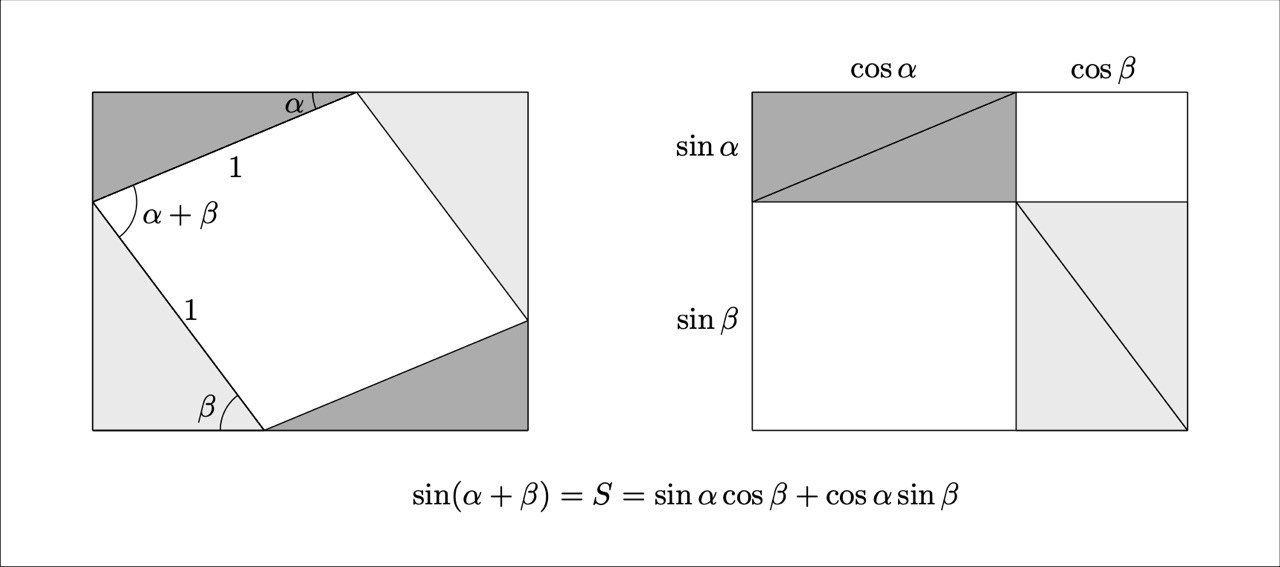
Наглядное доказательство формулы синуса суммы из книжки Ícons of Mathematics #картинка

Абдус Салам известен как отец пакистанского ядерного оружия и лауреат Нобелевской премии за теорию электрослабого взаимодействия. Но он был также блестящим математиком, что проявилось еще в юности. Вот одна из его ранних работ (ему тогда было 17 лет) — решение задачи Рамануджана, более эффективное, чем удалось найти самому Рамануджану
https://fermatslibrary.com/s/a-problem-of-ramanujan

Новым деканом мехмата МГУ избран Шафаревич Андрей, разумеется, Игоревич. Он выпускник физфака — такое, если не ошибаюсь, происходит с мехматом впервые. Сфера научных интересов А.И. также математическая физика — Навье, Стокс, и всё такое. Похоже, это тренд. Своего соперника, чистого математика, специалиста по банаховым пространствам Петра Бородина новый декан победил с преимуществом в голосах 88 против 13

Ну что, сделаем выборку более репрезентативнее? Самим же интересно будет
https://www.youtube.com/watch?v=2uTHGX_hrio

В этом ноябре могло бы исполниться 85 лет известному астрофизику и популяризатору науки Карлу Сагану, но увы — его нет с нами с 1996 г. Однако с нами остался целый ряд его неустаревающих работ, в частности, статья "Искусство определения вздора" — полезная ученым любых специальностей, да и не только ученым, а всем здравомыслящим людям. Полный текст на инглише по ссылке, а здесь несколько тезисов:

— Везде, где возможно, получайте независимое подтверждение фактов

— Поощряйте доказательные дебаты между сторонниками разных точек зрения

— Аргументы «авторитетных» специалистов имеют не больше веса, чем высказывания остальных участников дебатов. В науке нет понятия «авторитет», в крайнем случае здесь есть эксперты

— Не используйте только гипотезы и догадки. Если остались непонятные моменты, ищите для них объяснения, причём заходя с разных сторон. Затем придумайте, как проверить эти объяснения с помощью тестов и опровергнуть все, кроме одного — верного

— Не стоит упираться в идею только потому, что она ваша. Спросите себя, почему вы предпочитаете именно эту идею, сравните её с альтернативными, подумайте, что заставило бы вас отказаться от неё

https://www.inf.fu-berlin.de/lehre/pmo/eng/Sagan-Baloney.pdf

Кстати, неплохая задача для тестирования наклонностей — ученик с математическим складом ума спокойно ответит "голубого", а не закричит "да они все голубые!"

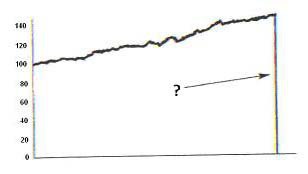
Всем, кто имеет дело с данными и статистикой, на День благодарения полезно вспомнить рассуждение Нассима Талеба из "Черного лебедя":

Представьте себе ход мыслей индейки, откармливаемой на убой. День ото дня ей дают всё больше зерна (как на графике), это продолжается 999 дней. Неглупая вроде бы птица делает вывод — тенденция продлится дальше. И вот тут-то ей, в четвертый четверг ноября, и отрубают голову.

Так что в статистике главное это понимание сути явления, а расчеты всяких там трендов — дело техники

Оказывается, многие люди испытывают ненависть к определителю матрицы только потому, что им в своё время толком не объяснили смысл и красоту этого понятия и заставили тупо зубрить громоздкую формулу. Прекрасно написал об этом Владимир Арнольд в статье "О преподавании математики":

Определитель матрицы — это (ориентированный) объём параллелепипеда, рёбра которого — её столбцы. Если сообщить студентам эту тайну (тщательно скрываемую в выхолощенном алгебраическом преподавании), то вся теория детерминантов становится понятной главой теории полилинейных форм. Если же определять детерминанты иначе, то у каждого разумного человека на всю жизнь останется отвращение и к определителям, и к якобианам, и к теореме о неявной функции

Статья Арнольда полностью: http://ega-math.narod.ru/Arnold2.htm

Несколько крышесносящая задачка из теории вероятностей:

У Алисы и Боба есть нечестные монеты, на которых с вероятностью 51% выпадает орел и 49% решка, по одной монете на каждого. Еще у них есть $100 начального капитала у каждого. По сигналу они начинают раз в минуту каждый ставить $1 на результат броска и бросать свою монету, причем Алиса всегда ставит на орла, а Боб всегда ставит на решку. Играют они против банка, а не против друг друга. Если кто-то разорился (у него кончились деньги), он выбывает из игры.

Известно, что в результате этой игры и Алиса и Боб разорились. Кто из них с большей вероятностью разорился первым?

Если вы решили эту задачу, то есть бонус-вопрос. Теперь у Алисы и Боба одна общая монета, и ее бросает судья, а ставят они как раньше, Алиса всегда на орла, Боб на решку. Монета, как и раньше, выпадает орлом с вероятностью 51%. Опять известно, что в конце концов они оба разорились. Кто с большей вероятностью разорился первым?

=========

Скажу сразу, что эта задачка нелегкая. Я сам ее решил неправильно; знаю правильное решение, но оно немного сломало мне мозг. Если хотите предложить свое решение, можно сделать это в чате канала; учтите, что там могут быть спойлеры.

ответ на первую задачу довольно удивительный: Алиса и Боб с одинаковой вероятностью разоряются первыми (и вообще, случайный процесс «как происходит игра у Алисы при условии, что она разоряется» совпадает с тем, как происходит игра у Боба)

https://avva.livejournal.com/3242391.html

В Москве проходит "Выставка фрактального искусства". Чтобы увидеть в некоторых произведениях фракталы, нужно недюжинное воображение. Но всё равно красиво

Спасибо рассылке The Bell — навела на интересную статью в Quanta Magazine о последних достижениях в деле доказательства гипотезы Коллатца. Пожалуй, это самая простая по формулировке проблема, над которой толпы дилетантов и специалистов тщетно бьются уже почти 90 лет. Но теперь за нее взялся Теренс Тао и кое-что открыл

Формулировка следующая. Берём натуральное число. Если оно чётное, делим его на два, а если нечётное — умножаем на три и добавляем единицу. Повторяем операцию. Гипотеза Лотара Коллатца состоит в том, что такая последовательность рано или поздно достигнет 1, ну а дальше зациклится: 1, 4, 2, 1, 4, 2, 1...

Хотите покрутить примеры — пожалуйста. Если хватит терпения, до 1 вы обязательно докрутите. Сейчас на компьютерах уже проверены все числа до квинтиллиона (18 нулей) с хвостом — и везде получилась единица. Но доказать корректно так и не удается. Многие математики считают, что не нужно и тратить драгоценное время сильных ученых на эту "игровую, искусственную" задачу, а лучше заниматься решением содержательных проблем.

Один из сильнейших математиков современности, Теренс Тао из Калифорнийского университета, в принципе так и делает, однако несколько дней в году все-таки посвящает решению "задач века". Однажды анонимный комментатор блога Тао посоветал ему   попробовать доказать гипотезу Коллатца не для всех натуральных чисел, а, так сказать, для "почти всех" — и Тао задумался.

Числа, которые мы подвергаем операциям Коллатца, как бы "пульсируют" — то возрастают, то убывают. Это напомнило Тао другие процессы, которые он изучал методами не теории чисел, а математической физики — пульсации жидкости, гравитации etc. Вот он и применил дифференциальные уравнения в частных производных к решению гипотезы Коллатца.

Результат, который получил Теренс Тао, в общих чертах звучит так: для "почти всех" чисел гипотеза Коллатца "почти справедлива". Чуть точнее: для 99% всех чисел (мы понимаем, что некорректно говорить о проценте от бесконечного количества, но понятно, что имеется в виду — 99% чисел в огромном отрезке натурального ряда) последовательность Коллатца достигает значения меньше 200.

Это лучшее достижение по гипотезе Коллатца, но его не совсем правильно называть прорывом, что подчеркивает и сам Тао — применение диффуров может позволить вам еще сильнее уточнить "процент" чисел, для которых гипотеза Коллатца верна, но к доказательству её в общем виде не приближает. Ждём озарений

https://www.quantamagazine.org/mathematician-terence-tao-and-the-collatz-conjecture-20191211/

http://www.sobaka.ru/city/city/101039

свежее интервью М.Я.Пратусевича (директора 239 школы)

Вы понимаете, почему самолёты летают? В общих чертах наверняка понимаете. Ну что там — профиль крыла таков, что частицам воздуха  над крылом нужно за то же время проходить большее расстояние, чем тем, которые обтекают профиль. Иначе поток разорвётся: интуитивно понятно — тут мы принимаем на веру — что такое невозможно. Значит, "верхние" частицы движутся быстрее "нижних". Значит, над крылом возникает разжение. Значит, нижний пласт будет выталкивать крыло вверх. Полетели! Никакой магии, только физика и математика

Но если вам хочется узнать про это подробнее, то вот ссылка на замечательную работу 1999 года:
https://fermatslibrary.com/s/how-airplanes-fly-a-physical-description-of-lift

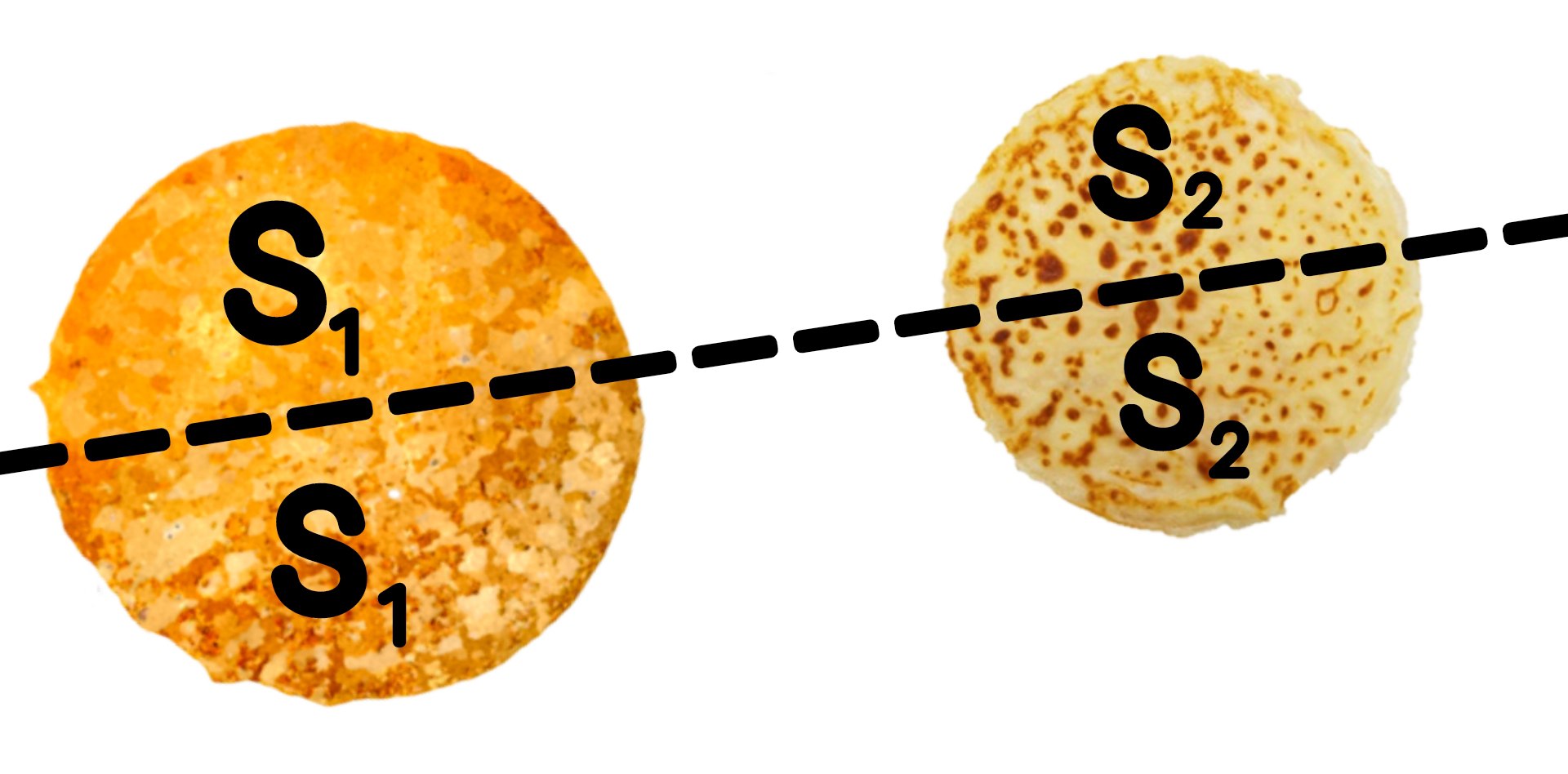
​​​​Теорема о блинах🥞

Теорема утверждает, что любые два блина (считаем их плоскими) всегда можно разрезать одним движением ножа так, чтобы каждый из них был разделен на две равные по площади части.

Другими словами через любые две фигуры лежащие в одной плоскости можно провести прямую так, чтобы она делила каждую из фигур на две равновеликие (равные по площади) фигуры.

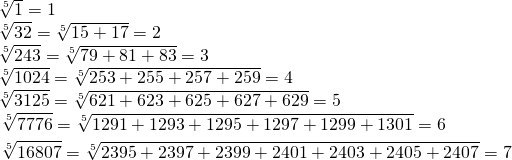
Красивая, казалось бы, штука — способ извлечения корня 5-й степени, когда известно, что он натуральное число. Представляем число под радикалом в виде суммы последовательных нечётных чисел, считаем количество слагаемых — вот оно и есть корень. Загвоздка в том, что непонятно, а с какого числа N начинать суммировать. С искомым корнем n оно связано формулой N = n^4 - (n-1) , но n-то мы и не знаем, а только собираемся найти