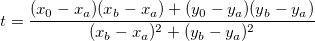CD
Size: a a a
2020 October 16
тебе даже не надо ничего делить в проверке попал или нет
CD
твоя проверка отработает для компьютерного нуля (проверь!)
I
ДА я верю, так-то. Я ответ то на свой вопрос уже давно получил.
I
тебе даже не надо ничего делить в проверке попал или нет
Именно.
I
Если ты про мою проверку, с параметром Т.
CD
Именно.
просто не выводи её из алгебраических уравнений, там заеба
CD
параметр T это просто скалярное произведение
CD
у тебя есть базис координат прямой, один из векторов который направляющий прямой, второй - его поворот на 90
CD
вот если его надо нормировать (скажем, расстояние по проекции, тонкая черная), то там надо проверять что это не вырожденная прямая
I
Вроде как ничего нормировать не надо. Ну в общем, вот как-то мне надо прийти к этому, я прихожу через Градиент.
I
У параболы на плоскости то взять градиент
I
это просто :)
CD
У параболы на плоскости то взять градиент
ну ты будешь через одно место выводить выражение (x-x0)*(x1-x0) + (y-y0)*(y1-y0) и все
2020 October 17
@N
А я просто использую параметрическое уравнение, и решаю уравнение множества всех расстояний
ты не "просто решаешь уравнение", ты заменил линейное (где бы просто нашёл проекцию точки на прямую) на кривую второго порядка: и вычислительно менее стабильнее и вообще неясно зачем
I
ты не "просто решаешь уравнение", ты заменил линейное (где бы просто нашёл проекцию точки на прямую) на кривую второго порядка: и вычислительно менее стабильнее и вообще неясно зачем
Ты ошибаешься.
I
Ну точнее, зачем, написано в диалоге с Костей. Остальное позже, в частности о стабильности и количестве действий не только с прямой.
БВ
I
ты не "просто решаешь уравнение", ты заменил линейное (где бы просто нашёл проекцию точки на прямую) на кривую второго порядка: и вычислительно менее стабильнее и вообще неясно зачем
Если я не ошибюаюсь, в решении у Кости, нам нужно делать деление.
I
В моем решении, деления нету. В нем вот так:
(a^2 + b^2)*t = a*x + b*y