В рейтинге участвует:

групп:

каналов:

Виртуальный сервер на SSD - недорого!

Аренда выделенных и виртуальных серверов (VDS/VPS), хостинг, аренда IP-адресов, администрирование, круглосуточная поддержка

qwarta.ru подробнее

Резервное копирование с проверкой на вирусы!!!

Удобный сервис создания резервных копий на любой сервер сети интернет. Отслеживайте изменения, проверяйте на вирусы. Надежно защитите свой бизнес!

go.backupland.com

Выбираете сервер? Любая конфигурация на заказ!

Аренда физических серверов любых конфигураций под любые запросы - 1С бухгалтерия, игровые сервера, нагруженные проекты, интернет-магазины!

qwarta.ru подробнее

Size: a a a

Теория категорий

559 membersпожаловаться на группу
2018 April 16

Oℕ

Oleg ℕizhnik in Теория категорий
Ну понятно, что про "функции" - это только там, где морфизмы можно так трактовать
источник
20:32пожаловаться#1

Oℕ

Oleg ℕizhnik in Теория категорий
Ну а колимит - это какое разбиение на классы какой-то возможно сильно бесконечной суммы. Такой, что для элементов из одного класса всегда выполняются указанные равенства.
И его "инициальность" означает что это самое точное такое разбиение
источник
20:35пожаловаться#2

VY

Vasiliy Yorkin in Теория категорий
источник
20:37пожаловаться#3

VY

Vasiliy Yorkin in Теория категорий
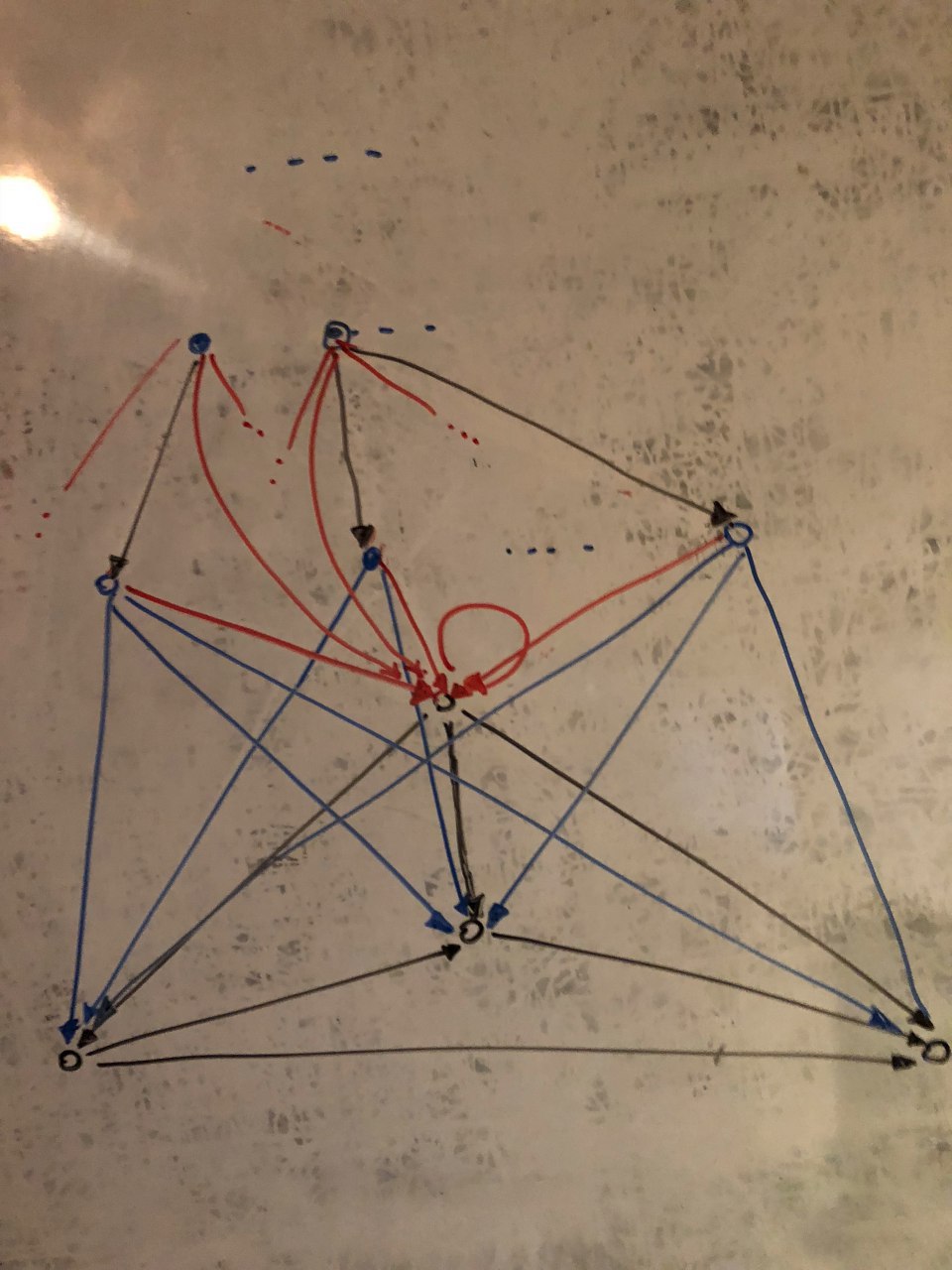
наверное, ничего не понятно что я пытался тут нарисовать
красные стрелки это факторизующие морфизмы
многотичия это типа значит что много таких конусов
вот эта точка сверху это вершина универсального конуса
источник
20:37пожаловаться#4

at

andrei tshurotshkin! 🎄 in Теория категорий
это стена или доска?
источник
20:37пожаловаться#5

Oℕ

Oleg ℕizhnik in Теория категорий
Vasiliy Yorkin
Непохоже на интуицию
источник
20:38пожаловаться#6

VY

Vasiliy Yorkin in Теория категорий
andrei tshurotshkin! 🎄
это стена или доска?
доска)
источник
20:39пожаловаться#7

AZ

Alex Zhukovsky in Теория категорий
Не совсем в тему, но спрошу : как доказать (или опровергнуть) что для любых различных простых чисел x y выполняется ax + by = 1 для целых a b?
источник
20:40пожаловаться#8

AZ

Alex Zhukovsky in Теория категорий
Ща в метро еду в голову пришло
источник
20:40пожаловаться#9

AZ

Alex Zhukovsky in Теория категорий
А придумать не получается
источник
20:40пожаловаться#10

VY

Vasiliy Yorkin in Теория категорий
Oleg ℕizhnik
Непохоже на интуицию
ну да, наверное, я просто не знаю что такое интуиция
(конструктивная/эмпирическая интуиция?)
нарисовал то, что преставляю, когда думаю о пределе
возможно, вообще не правильно, хотя это просто рисунок Бартоша, к которому я приделал всякой фигни сверху
upd: узнал что такое интуиция :)
источник
20:42пожаловаться#11

Oℕ

Oleg ℕizhnik in Теория категорий
Alex Zhukovsky
Не совсем в тему, но спрошу : как доказать (или опровергнуть) что для любых различных простых чисел x y выполняется ax + by = 1 для целых a b?
а вот недавно кок роз спрашивали про алгоритм Евклида
источник
20:48пожаловаться#12

Oℕ

Oleg ℕizhnik in Теория категорий
Alex Zhukovsky
Не совсем в тему, но спрошу : как доказать (или опровергнуть) что для любых различных простых чисел x y выполняется ax + by = 1 для целых a b?
для любых двух взаимно простых чисел не больше 2 выполняется - это 2 и 1
пусть выполняется для любых двух не больше n
тогда возмём x = n + 1 и взаимно-простой y поменьше, делим с остатком
x = d * y + r
y и r - взаимнопростые не больше n
находим
x * a1 + r * b1 = 1
выражаем
b = a1 - d * b1
a = b1
источник
20:55пожаловаться#13

ЗП

Зигохистоморфный Препроморфизм in Теория категорий
Oleg ℕizhnik
для любых двух взаимно простых чисел не больше 2 выполняется - это 2 и 1
пусть выполняется для любых двух не больше n
тогда возмём x = n + 1 и взаимно-простой y поменьше, делим с остатком
x = d * y + r
y и r - взаимнопростые не больше n
находим
x * a1 + r * b1 = 1
выражаем
b = a1 - d * b1
a = b1
мат индукция?)
источник
20:56пожаловаться#14

Oℕ

Oleg ℕizhnik in Теория категорий
К (не)счастью эти штуки школьного уровня приходилось регулярно воспроизводить. Деление в поле Zp для какого простого p  типа 1000000007 - рутинная операция в спортивном программировании
источник
21:00пожаловаться#15

AZ

Alex Zhukovsky in Теория категорий
Oleg ℕizhnik
К (не)счастью эти штуки школьного уровня приходилось регулярно воспроизводить. Деление в поле Zp для какого простого p  типа 1000000007 - рутинная операция в спортивном программировании
Ну то есть оно верно даже не для всех простых, а для любых взаимно простых?
источник
21:19пожаловаться#16

AZ

Alex Zhukovsky in Теория категорий
хорошее доказательство, спасибо
источник
21:19пожаловаться#17

Oℕ

Oleg ℕizhnik in Теория категорий
Alex Zhukovsky
Ну то есть оно верно даже не для всех простых, а для любых взаимно простых?
Оно верно для любой пары чисел. Просто справа должно стоять число, делящееся на их НОД
источник
21:20пожаловаться#18

Oℕ

Oleg ℕizhnik in Теория категорий
Ну и  не обязательно чисел. Многочленов и других всяческих колец.
источник
21:21пожаловаться#19

AZ

Alex Zhukovsky in Теория категорий
просто в книжке нашел упражнение доказать, что из двух взаимно простых чисел можно сформировать образующие для всех целых чисел
источник
21:21пожаловаться#20