NI
Size: a a a
2018 September 22
я это 100 раз говорил)
Труд хороший, классический, а повторить не жалко — вдруг кто ещё не видел? ;-)
ЗП
Труд хороший, классический, а повторить не жалко — вдруг кто ещё не видел? ;-)
Вармо Вене можно сказать отец RS или даже глобализатор и классификатор) Если не брать в счет труд Мейера
к
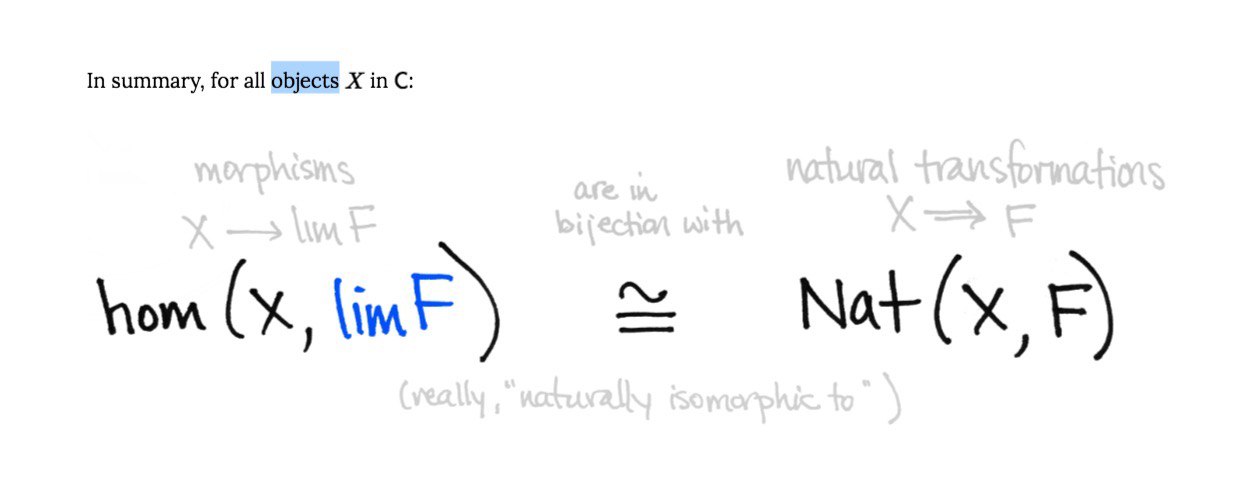
не могу понять этого утверждения, оно же не верно
к
- имеем индекс-категорию
- имеем категорию
- име
- имеем морфизм
- имеем два нат преобразования
получается два конуса из
они же не изоморфны. Или подразумевается, что alpha = beta . gamma? Тогда же любое такое множество будет единичным
I с объектами { 1, 2 }- имеем категорию
C с объектами { x, y, F 1, F 2 }F a - безымянные объекты/прообразы функтора F : I -> C- име
ем конст-функторы:
+ X : I -> C { X _ = x }
+ Y : I -> C { Y _ = y }- имеем морфизм
gamma : x -> y (по сути нат преобразование gamma : X -> Y)- имеем два нат преобразования
alpha : X -> F, beta : Y -> Fполучается два конуса из
X в F и из Y в F, lim F = Y, так как есть gamma
hom(X, lim F) = { gamma }
Nat(X, F) = { alpha, beta . gamma }они же не изоморфны. Или подразумевается, что alpha = beta . gamma? Тогда же любое такое множество будет единичным
к
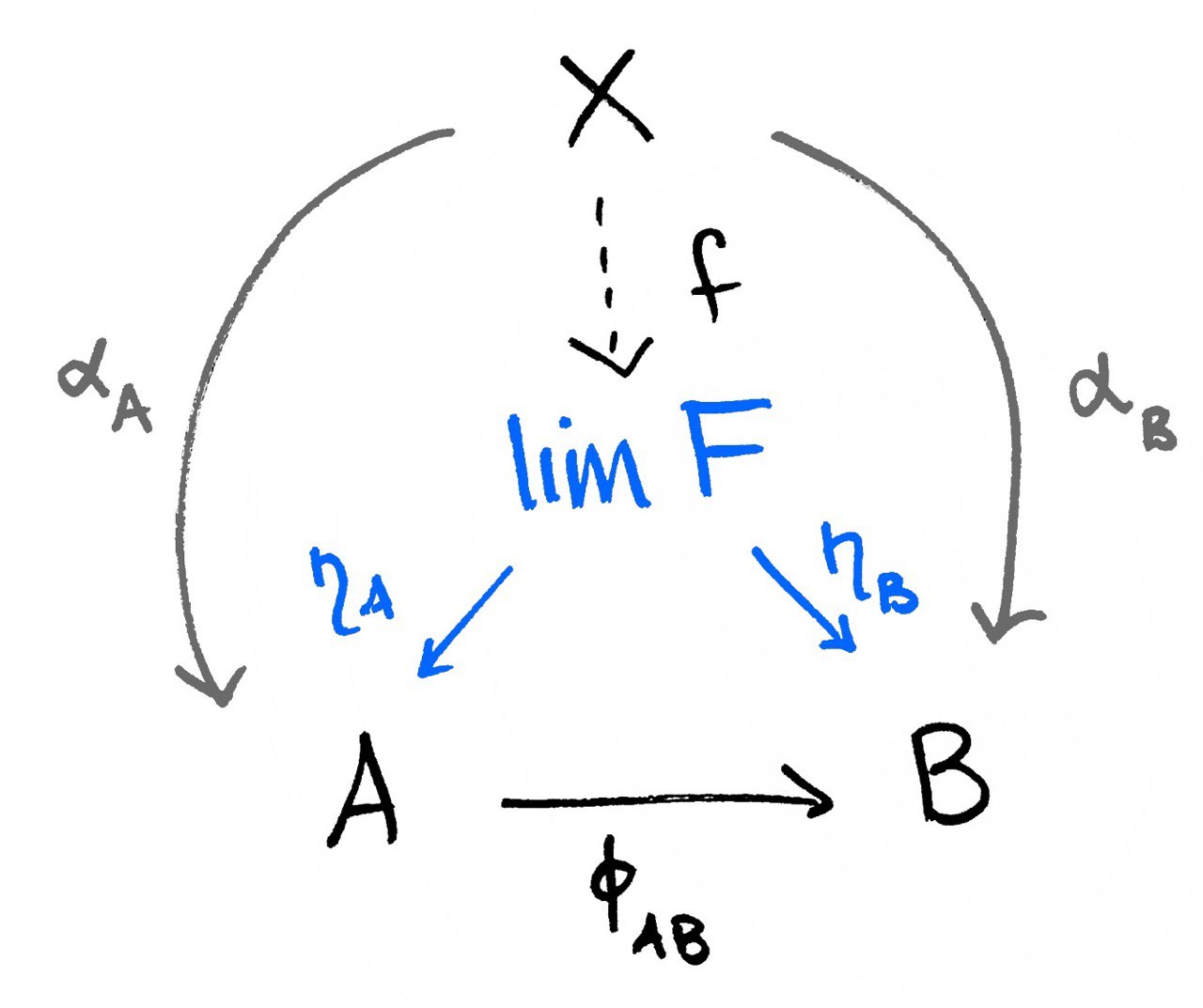
вот картинка даже, по ней видно, что
hom(X, lim F) = { f }
Nat(X, F) = { alpha, eta . f }к
Oℕ
- имеем индекс-категорию
- имеем категорию
- име
- имеем морфизм
- имеем два нат преобразования
получается два конуса из
они же не изоморфны. Или подразумевается, что alpha = beta . gamma? Тогда же любое такое множество будет единичным
I с объектами { 1, 2 }- имеем категорию
C с объектами { x, y, F 1, F 2 }F a - безымянные объекты/прообразы функтора F : I -> C- име
ем конст-функторы:
+ X : I -> C { X _ = x }
+ Y : I -> C { Y _ = y }- имеем морфизм
gamma : x -> y (по сути нат преобразование gamma : X -> Y)- имеем два нат преобразования
alpha : X -> F, beta : Y -> Fполучается два конуса из
X в F и из Y в F, lim F = Y, так как есть gamma
hom(X, lim F) = { gamma }
Nat(X, F) = { alpha, beta . gamma }они же не изоморфны. Или подразумевается, что alpha = beta . gamma? Тогда же любое такое множество будет единичным
alfa = beta . gamma вытекает из определения лимита
например как терминального объекта и определения морфизма в категории конусов
например как терминального объекта и определения морфизма в категории конусов
Oℕ
не любое
Oℕ
то же самое f - морфизм между конусами в вершинах X и lim F, тогда и только тогда, когда
forall a: { A, B}. alpha(a) = eta(a) . f
forall a: { A, B}. alpha(a) = eta(a) . f
2018 September 27
AG
Oℕ
NI
дЫк ещё надо про метрическое пространство, как про обогащёную категорию ;-)
NI
А вообще, тут рядом во вполне так классике есть "соответствие Галуа" (Galois connection).
Это сопряжение между предпорядками.
Это сопряжение между предпорядками.
AG
ну да соответствия галуа это архетипические сопряжения
NI
Краткий вывод озвучен неоднократно —
учитесь понимать сопряжённости ;-)
учитесь понимать сопряжённости ;-)
2018 September 28
a
Достаточно приятно осознавать тот факт, что струнные диаграммы есть не только прелесть нотации, а сами по себе являются n-мерными кобордизмами и их выпрямления формально доказываются гомотопиями функций Морзе.
AG
этот факт же жояль со стритом в первой же статье доказали как теорему
NI
Достаточно приятно осознавать тот факт, что струнные диаграммы есть не только прелесть нотации, а сами по себе являются n-мерными кобордизмами и их выпрямления формально доказываются гомотопиями функций Морзе.
Таки обычно говорят по-русски "Морса" —
https://ru.wikipedia.org/wiki/Теория_Морса
Хотя и известные коды таки "Морзе", почему-то.
По-английски, пишется одинаково.
https://ru.wikipedia.org/wiki/Теория_Морса
Хотя и известные коды таки "Морзе", почему-то.
По-английски, пишется одинаково.
2018 October 02