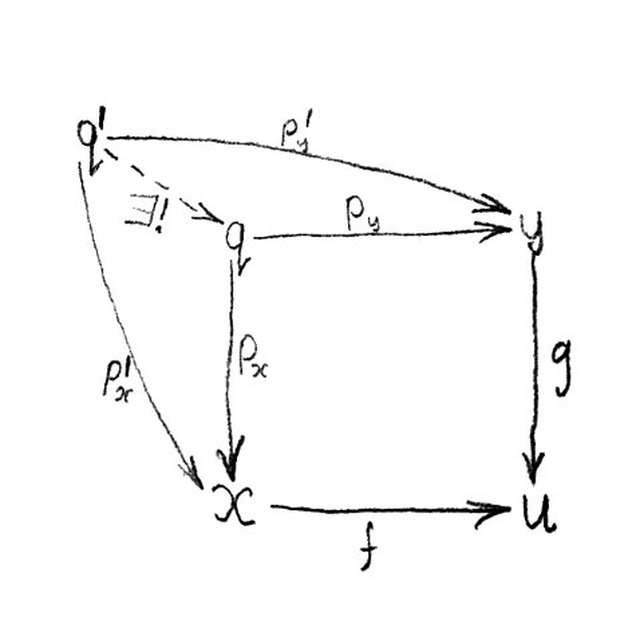
PS
Size: a a a
2019 January 08
все эти конструкции выражаются и исследуются через опетопы, а это высшая теория категорий, так что я бы не сказал что это оффтоп. но дело ваше
EP
все эти конструкции выражаются и исследуются через опетопы, а это высшая теория категорий, так что я бы не сказал что это оффтоп. но дело ваше
вот именно, причём успешно
иначе возникает вопрос что есть абстрактаная теория категорий где это не нужно
иначе возникает вопрос что есть абстрактаная теория категорий где это не нужно
MK
Emelian Piker (Евгений)
на самом деле полукольца это действительно моноиды, но моноиды это не полукольца, полугруппа вот тоже моноид, полугруппа это не полукольцо
У меня был вопрос относительно того, чем же все таки по-настоящему, является полукольцо. Если оно должно содержать единичный и нулевой элемент для определенной бинарной операции - хорошо, но как тогда называется та самая та штука, которая не имеет этих элементов? Rig - это без единичного элемента, как тогда будет без еще и нулевого?
EP
надо табличку составить и декларировать определение в теории категорий, названия лупа и моноид это всётаки модерн, полугруппа с нейтральным элементом это более понятно
EP
У меня был вопрос относительно того, чем же все таки по-настоящему, является полукольцо. Если оно должно содержать единичный и нулевой элемент для определенной бинарной операции - хорошо, но как тогда называется та самая та штука, которая не имеет этих элементов? Rig - это без единичного элемента, как тогда будет без еще и нулевого?
там аддитивы и мультипликативы, вопрос, так это декларируется в теории категорий
EP
я понимаю что там типо будет продукт из теории категорий, вопрос для чего, для мультипликпьива, а для аддитива что тогда ?
PS
Emelian Piker (Евгений)
надо табличку составить и декларировать определение в теории категорий, названия лупа и моноид это всётаки модерн, полугруппа с нейтральным элементом это более понятно
Ring-like structures or Ringoids: two binary operations, often called addition and multiplication, with multiplication distributing over addition.
Semiring: a ringoid such that S is a monoid under each operation. Addition is typically assumed to be commutative and associative, and the monoid product is assumed to distribute over the addition on both sides, and the additive identity satisfies 0 x = 0 for all x.
Near-ring: a semiring whose additive monoid is a (not necessarily abelian) group.
Ring: a semiring whose additive monoid is an abelian group.
Lie ring: a ringoid whose additive monoid is an abelian group, but whose multiplicative operation satisfies the Jacobi identity rather than associativity.
Boolean ring: a commutative ring with idempotent multiplication operation.
Field: a commutative ring which contains a multiplicative inverse for every nonzero element
Kleene algebras: a semiring with idempotent addition and a unary operation, the Kleene star, satisfying additional properties.
*-algebra: a ring with an additional unary operation (*) satisfying additional properties.
Semiring: a ringoid such that S is a monoid under each operation. Addition is typically assumed to be commutative and associative, and the monoid product is assumed to distribute over the addition on both sides, and the additive identity satisfies 0 x = 0 for all x.
Near-ring: a semiring whose additive monoid is a (not necessarily abelian) group.
Ring: a semiring whose additive monoid is an abelian group.
Lie ring: a ringoid whose additive monoid is an abelian group, but whose multiplicative operation satisfies the Jacobi identity rather than associativity.
Boolean ring: a commutative ring with idempotent multiplication operation.
Field: a commutative ring which contains a multiplicative inverse for every nonzero element
Kleene algebras: a semiring with idempotent addition and a unary operation, the Kleene star, satisfying additional properties.
*-algebra: a ring with an additional unary operation (*) satisfying additional properties.
PS
например. полезных структур много, и некоторый бардак в соглашениях "кольцо" vs "кольцо с единицей" есть. с практической точки зрения я соглашусь с утверждением выше, что не стоит никому доверять :)
MK
Ring-like structures or Ringoids: two binary operations, often called addition and multiplication, with multiplication distributing over addition.
Semiring: a ringoid such that S is a monoid under each operation. Addition is typically assumed to be commutative and associative, and the monoid product is assumed to distribute over the addition on both sides, and the additive identity satisfies 0 x = 0 for all x.
Near-ring: a semiring whose additive monoid is a (not necessarily abelian) group.
Ring: a semiring whose additive monoid is an abelian group.
Lie ring: a ringoid whose additive monoid is an abelian group, but whose multiplicative operation satisfies the Jacobi identity rather than associativity.
Boolean ring: a commutative ring with idempotent multiplication operation.
Field: a commutative ring which contains a multiplicative inverse for every nonzero element
Kleene algebras: a semiring with idempotent addition and a unary operation, the Kleene star, satisfying additional properties.
*-algebra: a ring with an additional unary operation (*) satisfying additional properties.
Semiring: a ringoid such that S is a monoid under each operation. Addition is typically assumed to be commutative and associative, and the monoid product is assumed to distribute over the addition on both sides, and the additive identity satisfies 0 x = 0 for all x.
Near-ring: a semiring whose additive monoid is a (not necessarily abelian) group.
Ring: a semiring whose additive monoid is an abelian group.
Lie ring: a ringoid whose additive monoid is an abelian group, but whose multiplicative operation satisfies the Jacobi identity rather than associativity.
Boolean ring: a commutative ring with idempotent multiplication operation.
Field: a commutative ring which contains a multiplicative inverse for every nonzero element
Kleene algebras: a semiring with idempotent addition and a unary operation, the Kleene star, satisfying additional properties.
*-algebra: a ring with an additional unary operation (*) satisfying additional properties.
О, спасибо, выходит что это кольцоиды.
NI
EP
Возникает вопрос что такое тогда ко бипродукт, аддитивная конюнкция ?
EP
EP
можете представить себе некомутативное асоциативное сложение ? кстати в языках програмирования есть такой case, есть также операция http://hackage.haskell.org/package/base-4.12.0.0/docs/Control-Applicative.html#t:Alternative
EP
по идее вот этот alternative из хаскеля это бипродукт, кейс это типа ко бипродукт, композиция кейс паттернов может быть асоциативной и некомутативной
EP
это всё както намекает на связь линейной логики и теории категорий
EP
2019 January 09
AG
Emelian Piker (Евгений)
это всё както намекает на связь линейной логики и теории категорий
связь там известна
AG
описана в обзорной статье Мельеса наиболее полно
2019 January 12
EP
связь там известна
класс, возникает вопрос где сейчас и в каких программах или предметах эта связь наилучшим образом используется
EP
описана в обзорной статье Мельеса наиболее полно
это здорово, наверно не только там, вопрос в том с чего начать и как лучше усвоить, или возможно даже найти хорошие паралели в практических примерах