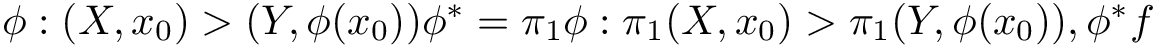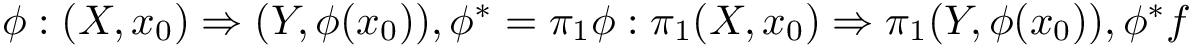AG
Size: a a a
2018 March 03
P
как тогда этот функтор отображает непрерывное отображение в гомоморфизм межуд фундаментальными группами?
а, ну это работает вот так: \phi : (X, x_0) —> (Y, \phi(x_0)) индуцирует отображение \phi^{*} = \pi_1\phi : \pi_1(X,x_0) —> \pi_1(Y,\phi(x_0)), где \phi^{*} \[f\] = \[\phi f\]. \phi^{*} зависит только от гомотопического класса \phi и равенства вида (\phi_1\phi_2)^{*} = (\phi_1)^{*}(\phi_2)^{*} и (1_(X,x_0))^{*} = 1_{\pi(X,x_0)}
P
тут нет техбота?
Oℕ
в тг есть техбот?
P
ваще да, я видел
P
в чате нму вроде был
Oℕ
как он работает? у тебя же даже там долларов нет вокруг
P
а нет, в инфернале
P
это да, я их не ставил, чтоб работал надо формулы отдельными сообщениями
P
и он картинки пришлет
Oℕ
а нет, в инфернале
нет, и там не сработало
P
/convert@LatexBot
P
епт, ща
Oℕ
/convert@LatexBot
Oℕ
/convert@LatexBot \phi : (X, x_0) —> (Y, \phi(x_0)) индуцирует отображение \phi^{*} = \pi_1\phi : \pi_1(X,x_0) —> \pi_1(Y,\phi(x_0)), где \phi^{*} \[f\] = \[\phi f\]. \phi^{*} зависит только от гомотопического класса \phi и равенства вида (\phi_1\phi_2)^{*} = (\phi_1)^{*}(\phi_2)^{*} и (1_(X,x_0))^{*} = 1_{\pi(X,x_0)}
P
/convert@LatexBot $ \phi : (X, x_0) \Rightarrow (Y, \phi(x_0)) $, $ \phi^{*} = \pi_1\phi : \pi_1(X,x_0) \Rightarrow \pi_1(Y,\phi(x_0)) $, $\phi^{*} \[f\] = \[\phi f\]. \phi^{*}$, $(\phi_1\phi_2)^{*} = (\phi_1)^{*}(\phi_2)^{*} и (1_(X,x_0))^{*} = 1_{\pi(X,x_0)}$