Size: a a a
2018 December 16
2018 December 24

Семинар в МЦНМО
В четверг 27 декабря на новогоднем заседании семинара учителей математики Николай Андреев, Николай Петрович Долбилин и Никита Панюнин будут рассказывать про математическую составляющую изображения мира на плоскости — и про карты, и про картины.
С 19:00, в столовой МЦНМО на 1 этаже.
https://mccme.ru/nir/seminar
В четверг 27 декабря на новогоднем заседании семинара учителей математики Николай Андреев, Николай Петрович Долбилин и Никита Панюнин будут рассказывать про математическую составляющую изображения мира на плоскости — и про карты, и про картины.
С 19:00, в столовой МЦНМО на 1 этаже.
https://mccme.ru/nir/seminar
2018 December 26

Калейдоскоп
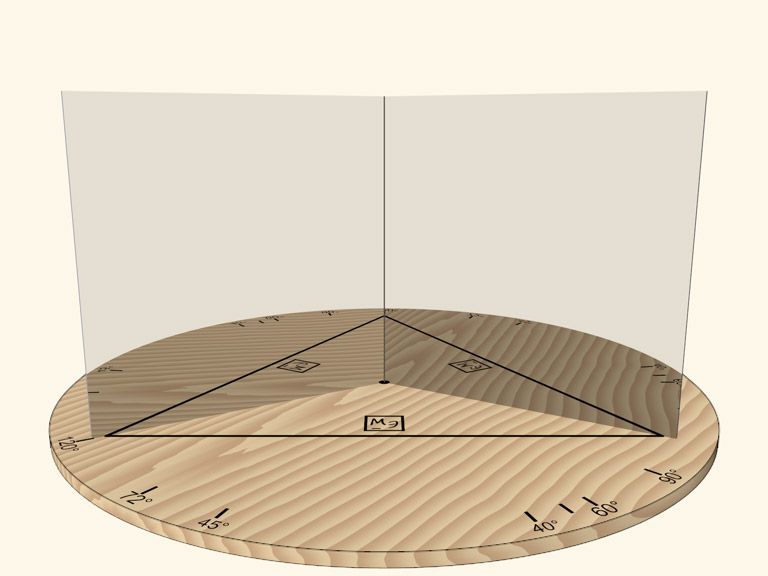
Два зеркала, поставленные как распахнутая книжка, показывают, как работают калейдоскопы. Отражение зеркала в зеркале снова работает как зеркало.
На сайте математических этюдов новое видео: эти два зеркала крутят и видно, как отражается отрезок.
Два зеркала, поставленные как распахнутая книжка, показывают, как работают калейдоскопы. Отражение зеркала в зеркале снова работает как зеркало.
На сайте математических этюдов новое видео: эти два зеркала крутят и видно, как отражается отрезок.
2018 December 31

Этот постер был тут уже год назад, но вдруг у кого-то его нет.

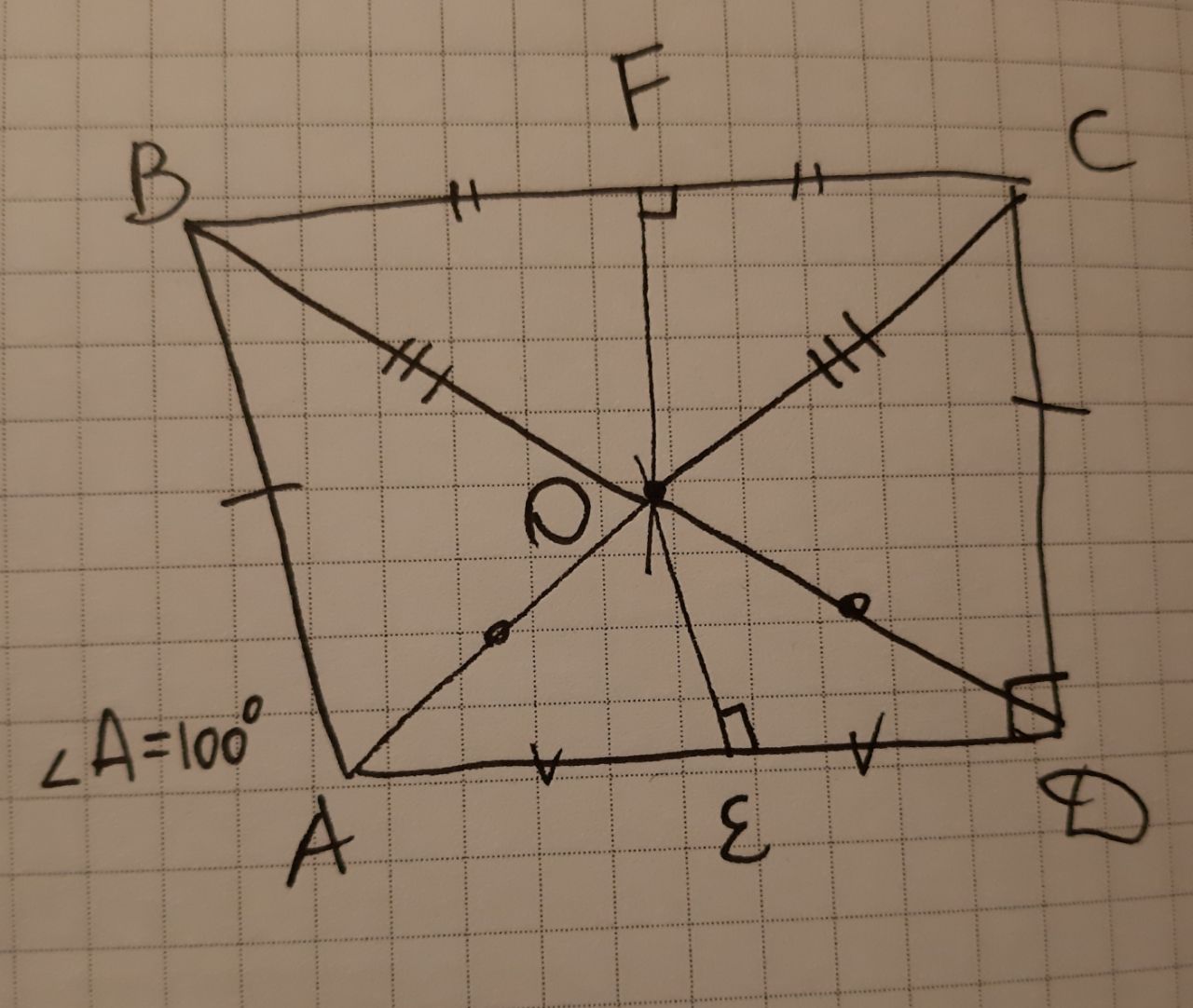
306. В четырехугольнике ABCD: ∠A=100°, ∠D=90°, AB=CD. Серединные перпендикуляры к BC и AD пересекаются в точке O.
O лежит на этих перпендикулярах, поэтому OB=OC, AO=OD. Отсюда треугольники ABO и CDO равны по трем сторонам, а также ∠OAD=∠ODA. Получается, что ∠A=∠D.
Эй, а как же 100° и 90°?
#задача
O лежит на этих перпендикулярах, поэтому OB=OC, AO=OD. Отсюда треугольники ABO и CDO равны по трем сторонам, а также ∠OAD=∠ODA. Получается, что ∠A=∠D.
Эй, а как же 100° и 90°?
#задача
2019 January 03

Семинар в МЦНМО
В четверг 10 января в 19:00 семинар учителей.
Г.Б.Филипповский «Геометрическая миниатюра как приглашение к разговору».
Докладчик годами собирал красивые задачи, объединял их в миниатюры и теперь предлагает их обсудить и встретить новые задачи и конструкции.
Докладчик представит несколько миниатюр: «Сравним отрезок прямой Эйлера с отрезком формулы Эйлера», «Угол между медианой и стороной решает задачу», «Когда один отрезок равен сумме двух других» и другие.
https://www.mccme.ru/nir/seminar/
В четверг 10 января в 19:00 семинар учителей.
Г.Б.Филипповский «Геометрическая миниатюра как приглашение к разговору».
Докладчик годами собирал красивые задачи, объединял их в миниатюры и теперь предлагает их обсудить и встретить новые задачи и конструкции.
Докладчик представит несколько миниатюр: «Сравним отрезок прямой Эйлера с отрезком формулы Эйлера», «Угол между медианой и стороной решает задачу», «Когда один отрезок равен сумме двух других» и другие.
https://www.mccme.ru/nir/seminar/
2019 January 05

Новогодняя головоломка Катрионы Ширер
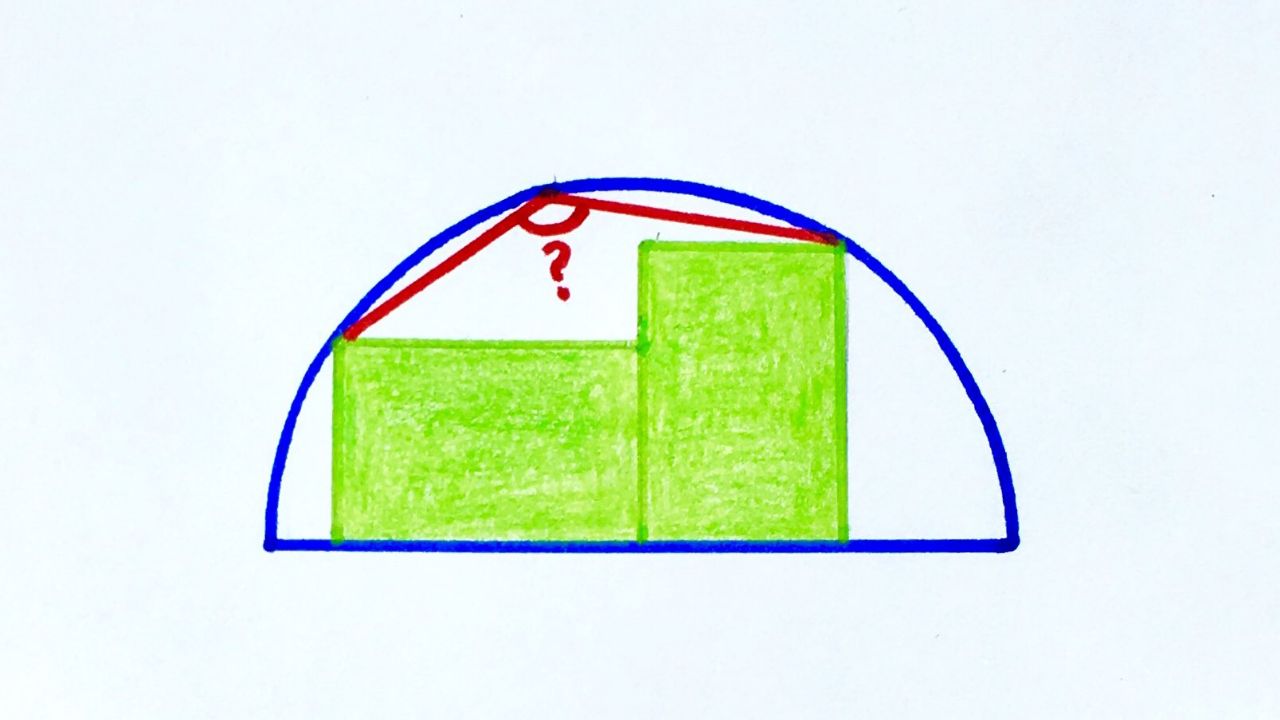
Два равных прямоугольника вписаны в полукруг. Надо найти красный угол.
Эта и другие головоломки в твитере Катрионы
Два равных прямоугольника вписаны в полукруг. Надо найти красный угол.
Эта и другие головоломки в твитере Катрионы
2019 January 06
2019 January 10

Мастеркласс по работе с Геогеброй
Алексей Сгибнев выложил мастеркласс по первой главе своей книги «Геометрия на подвижных чертежах».
Смотрите видео
С 01:00 – урок с 6-классниками,
с 22:25 – обсуждение с учителями,
с 43:40 – окончание урока.
Рекомендую учителям математики и тем, кто еще не пробовал работать с Геогеброй.
#видео
Алексей Сгибнев выложил мастеркласс по первой главе своей книги «Геометрия на подвижных чертежах».
Смотрите видео
С 01:00 – урок с 6-классниками,
с 22:25 – обсуждение с учителями,
с 43:40 – окончание урока.
Рекомендую учителям математики и тем, кто еще не пробовал работать с Геогеброй.
#видео
2019 January 12

307. В выпуклом четырехугольнике АВСD длина отрезка, соединяющего середины сторон АВ и СD, равна 1 метру. Прямые АD и ВС перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей АС и ВD.
#задача
#задача
2019 January 13

https://youtu.be/HEfHFsfGXjs
новое видео от 3Blue1Brown про удивительное появление pi при подсчете числа соударений шаров разной массы
придумал эту систему Г.Гальперин, вот его статья в МатПросвещении http://mi.mathnet.ru/mp826
новое видео от 3Blue1Brown про удивительное появление pi при подсчете числа соударений шаров разной массы
придумал эту систему Г.Гальперин, вот его статья в МатПросвещении http://mi.mathnet.ru/mp826
2019 January 14

Вот несколько из задач на условную тему «x=y+z», про которые Г.Б.Филипповский рассказывал на семинаре учителей в прошедший четверг.
i) В равнобедренном треугольнике сумма расстояний от произвольной точки на основании до боковых сторон равна высоте.
ii) Проведем через центр вписанной окружности прямоугольного треугольника прямые, параллельные сторонам. Сумма двух отрезков, высекаемых на катетах, равна отрезку, высекаемому на гипотенузе.
iii) Проведем произвольную прямую через точку пересечения медиан треугольника. Сумма расстояний от нее до двух вершин равна расстоянию до третьей.
iv) Впишем в треугольник окружность и посмотрим на расстояния от точек касания до середин соответствующих сторон. Сумма двух из них равна третьему.
v) Для точки на описанной окружности правильного треугольника сумма расстояний до двух вершин равна расстоянию до третьей.
vi) Зафиксируем какую-нибудь окружность, касающуюся описанной окружности правильного треугольника, и проведем к этой окружности касательные из вершин треугольника. Сумма двух из касательных равна третьей.
У каждой есть короткое и симпатичное решение — попробуйте.
i) В равнобедренном треугольнике сумма расстояний от произвольной точки на основании до боковых сторон равна высоте.
ii) Проведем через центр вписанной окружности прямоугольного треугольника прямые, параллельные сторонам. Сумма двух отрезков, высекаемых на катетах, равна отрезку, высекаемому на гипотенузе.
iii) Проведем произвольную прямую через точку пересечения медиан треугольника. Сумма расстояний от нее до двух вершин равна расстоянию до третьей.
iv) Впишем в треугольник окружность и посмотрим на расстояния от точек касания до середин соответствующих сторон. Сумма двух из них равна третьему.
v) Для точки на описанной окружности правильного треугольника сумма расстояний до двух вершин равна расстоянию до третьей.
vi) Зафиксируем какую-нибудь окружность, касающуюся описанной окружности правильного треугольника, и проведем к этой окружности касательные из вершин треугольника. Сумма двух из касательных равна третьей.
У каждой есть короткое и симпатичное решение — попробуйте.

Семинар в МЦНМО
https://www.mccme.ru/nir/seminar/
24 января в 19:00
В.В.Прасолов «Новая серия сборников задач для 7–11 классов»
Доклад посвящён новому проекту: сборникам задач немного повышенной сложности, приспособленных для работы в школе, с разбивкой по классам.
У предыдущих сборников задач цели другие: они предназначены для школьников, уже знакомых со школьной программой и желающих научиться решать трудные задачи. Никакой разбивки по классам в них нет, и они не предназначены для того, чтобы прорешать их полностью.
Новый задачник по планиметрии уже издан, остальные (в том числе задачники по алгебре) ещё пишутся или готовятся к изданию.
К задачнику по геометрии для 7 класса есть сопровождающая книга для чтения, о ней Виктор Васильевич тоже расскажет.
https://www.mccme.ru/nir/seminar/
24 января в 19:00
В.В.Прасолов «Новая серия сборников задач для 7–11 классов»
Доклад посвящён новому проекту: сборникам задач немного повышенной сложности, приспособленных для работы в школе, с разбивкой по классам.
У предыдущих сборников задач цели другие: они предназначены для школьников, уже знакомых со школьной программой и желающих научиться решать трудные задачи. Никакой разбивки по классам в них нет, и они не предназначены для того, чтобы прорешать их полностью.
Новый задачник по планиметрии уже издан, остальные (в том числе задачники по алгебре) ещё пишутся или готовятся к изданию.
К задачнику по геометрии для 7 класса есть сопровождающая книга для чтения, о ней Виктор Васильевич тоже расскажет.
2019 January 21

2019 January 26


картинка по выходным: рогатая сфера Александера (рис. А.Т.Фоменко)
прочитать про нее можно в статье Д.Б.Фукса в Кванте: http://kvant.mccme.ru/1990/06/rogataya_sfera_aleksandera.htm
прочитать про нее можно в статье Д.Б.Фукса в Кванте: http://kvant.mccme.ru/1990/06/rogataya_sfera_aleksandera.htm
2019 February 04

Это условия регионального этапа Всероссийской олимпиады по математике
2019 February 06

Задачи по геометрии со всех олимпиад: https://imogeometry.blogspot.com/p/blog-page_2.html