Автором задачи 34 является Архимед. Когда в середине 1980-х редакция «Кванта» объявила конкурс среди авторов на лучшую задачу, которую можно будет опубликовать в задачнике под номером 1000, она получила массу новых и интересных задач, но в итоге была выбрана именно задача Архимеда. Решение — http://kvant.mccme.ru/1986/12/p32.htm

Еще два красивых доказательства этого факта (по-английски, кстати, он красиво называется «Теорема о сломанной хорде»):
http://www.cut-the-knot.org/triangle/BrokenChordBQT.shtml#proof
и http://www.cut-the-knot.org/triangle/BrokenChordmpdlc.shtml#proof

Сегодняшняя задача навеяна своим номером.

35. Найдите углы четырехугольника ABCD, если угол CBD равен 35°, угол ABD равен 65°, угол ADC равен 130°, а BC=BA.

Идея решения задачи 35: раз BC=BA, то точки A и C лежат на окружности с центром B. Докажем, что и D лежит на этой же окружности. Это следует из того, что угол 130° равен половине от (360°–35°–65°), то есть половине центрального угла. Следовательно, он вписанный...
Ну а дальше всё просто: треугольники ABD и DBC равнобедренные, а по углу при вершине легко находим углы при основании.

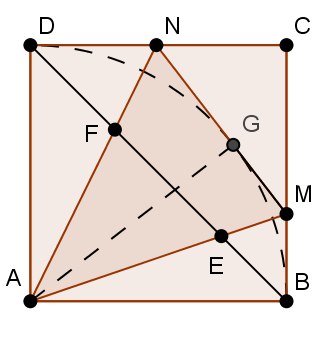
36. Треугольник AMN с углом A=45° вписан в квадрат ABCD так, что M лежит на BC, а N лежит на CD. В каком отношении диагональ BD делит площадь этого треугольника?

Ответ на задачу 36: диагональ делит треугольник на две равные по площади части (AEF и EFNM на рисунке).

Будем рассматривать эту картинку как результат сгибания листа бумаги — сначала перегнём треугольник AMB по гипотенузе AM, потом перегнём треугольник AND по гипотенузе AN. Так как при сгибании сумма углов при вершине А уменьшится вдвое, то в результате AB совместится с AD, а точки D и B попадут в одну точку G — основание высоты треугольника AMN.

Далее, угол AEF = 45° + EAB = 45° + EAG = 135° – AMG = 180° – MAN – AMN = ANM, и аналогично, равны углы AFE и AMN. Поэтому треугольник AEF подобен треугольнику AMN.

А так как высота AG в  треугольнике AMN равна стороне квадрата, а высота из вершины A в треугольнике AEF равна половине диагонали, то коэффициент подобия равен 1/√2. Следовательно, отношение площадей AEF и AMN равно 1/2.

До ответа в задаче 36 легко догадаться, выбрав точки так: M = B, N = C.

Спасибо большое Косте за интересную неделю. Канал уходит на выходные. Следующая задачка 27 февраля.

37. На сторонах треугольника ABC во внешние стороны построены три правильных треугольника. Докажите, что их центры D, E, F являются вершинами четвёртого правильного треугольника. Это первая часть теоремы Эшера.

Вторая часть теоремы — шестиугольниками, равными AFBDCE, можно замостить плоскость.

Теорема Эшера навеяна вот этим знаменитым рисунком:

Решение «еженедельного гроба», задачи 30:
http://telegra.ph/Reshenie-Zadachi-30-02-28

Гроб#3 ждите сегодня вечером.

38, Еженедельный гроб #3
http://telegra.ph/Grob3-02-28

39. Из квадрата 5×5 вырезали центральную клетку. Разрежьте получившуюся фигуру на две части, в которые можно завернуть куб 2×2×2.

Автор: Сергей Иванович Токарев
Источник: Математический праздник 1998 года

Решение задачи 39