AG
Size: a a a
2018 May 01
VS
есть даже записи видео за вчера и сегодня, правда сырые
did you mean video? where?
VS
Ok, thanks!
AG
ну и остальные тоже у этого же чела в аккаунте
AG
они живьём транслируют, можно завтра посмотреть например ;)
2018 May 02
к
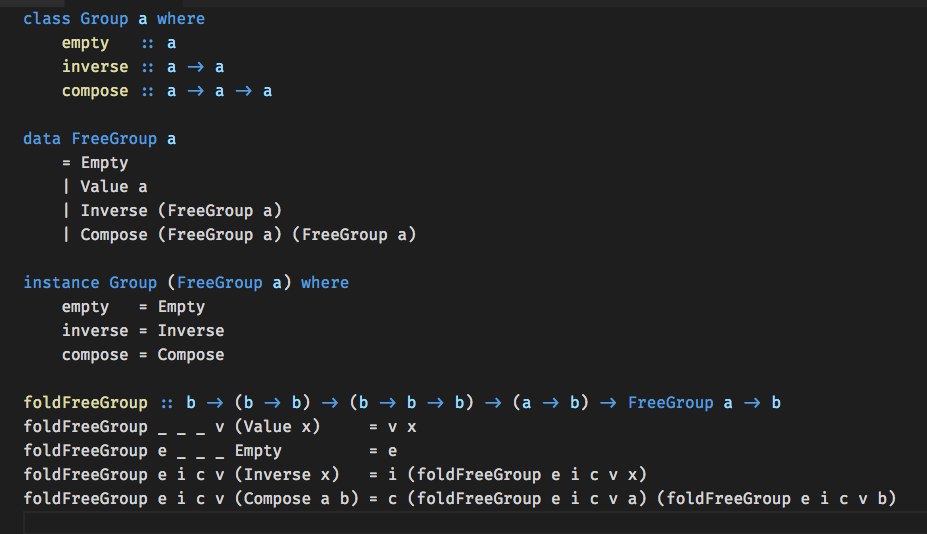
сильно не по теме, но давно крутится некоторая мысль о том, что свободная алгебраическая структура - что-то вроде ленивой версии других несвододных структур, где вместо самой операций мы просто используем конструкторы.
А после добавления соотношений между этими конструкторами и другими элементами множеств (интерпретатор по сути) мы получаем уже несвободную структуру. То есть свободные структуры свободны от интерпретатора)
Таким образом любое представление каких-нибудь данных представляет из себя свободные версии результатов интерпретации этих данных
А после добавления соотношений между этими конструкторами и другими элементами множеств (интерпретатор по сути) мы получаем уже несвободную структуру. То есть свободные структуры свободны от интерпретатора)
Таким образом любое представление каких-нибудь данных представляет из себя свободные версии результатов интерпретации этих данных
к
к
сильно не по теме, но давно крутится некоторая мысль о том, что свободная алгебраическая структура - что-то вроде ленивой версии других несвододных структур, где вместо самой операций мы просто используем конструкторы.
А после добавления соотношений между этими конструкторами и другими элементами множеств (интерпретатор по сути) мы получаем уже несвободную структуру. То есть свободные структуры свободны от интерпретатора)
Таким образом любое представление каких-нибудь данных представляет из себя свободные версии результатов интерпретации этих данных
А после добавления соотношений между этими конструкторами и другими элементами множеств (интерпретатор по сути) мы получаем уже несвободную структуру. То есть свободные структуры свободны от интерпретатора)
Таким образом любое представление каких-нибудь данных представляет из себя свободные версии результатов интерпретации этих данных
под любым представлением данных я имею в виду любое представление данных в виде конструкторов (а это значит, что наверное любое вообще), ведь даже foldr (+) 0 [1, 2, 3] это по сути сначала свободное представление 6 как структуры
Cons 1 (Cons 2 (Cons 3 Nil), а потом замена Cons на +, а Nil на 0к
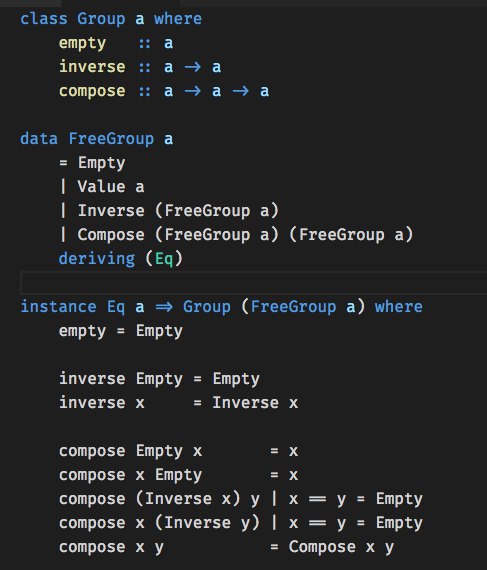
полагаю вот такое тоже допустимо для опредения свободной группы, так как отношения есть в определении
к
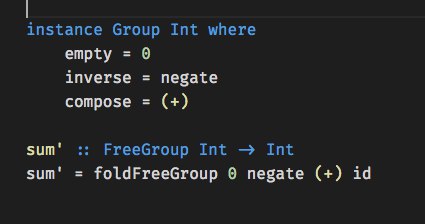
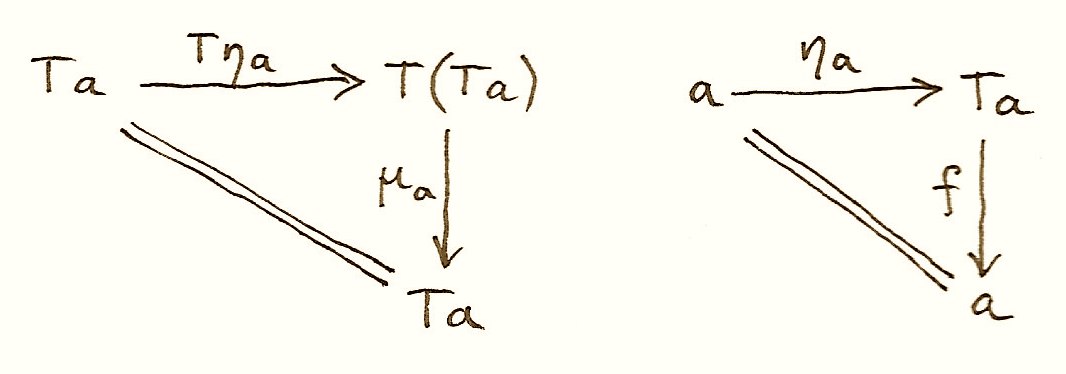
а так же интересно, что свободная группа + интерпретатор и сразу интерпретатор по сути представляю из себя два изоморфных способа писать интерпретаторы: начальный и финальный
VS
сильно не по теме, но давно крутится некоторая мысль о том, что свободная алгебраическая структура - что-то вроде ленивой версии других несвододных структур, где вместо самой операций мы просто используем конструкторы.
А после добавления соотношений между этими конструкторами и другими элементами множеств (интерпретатор по сути) мы получаем уже несвободную структуру. То есть свободные структуры свободны от интерпретатора)
Таким образом любое представление каких-нибудь данных представляет из себя свободные версии результатов интерпретации этих данных
А после добавления соотношений между этими конструкторами и другими элементами множеств (интерпретатор по сути) мы получаем уже несвободную структуру. То есть свободные структуры свободны от интерпретатора)
Таким образом любое представление каких-нибудь данных представляет из себя свободные версии результатов интерпретации этих данных
пытаюсь понять, что вы хотели сказать на уровне диаграмм
VS
G -> (forgetful) F -> (interpreter) G
| |
V V
(lazy) (lazy)
G(l) F(l)
| |
V V
(lazy) (lazy)
G(l) F(l)
VS
(forgetful) and (interpreter) are functors
VS
whether (lazy) in G->(lazy)G(l) and in F->(lazy)F(l) are functors or not, don't know
VS
и никак не могу понять полезность обращения к lazyness, вроде G -> (forgetful) F -> (interpreter) G вполне достаточно
Oℕ
Из праздного интереса: как выглядят экспоненциальные объекты в 2-категориях?
Oℕ
И бывает ли так, что для 1-морфизмов нет экспоненциальных объектов, а для 2- есть?
NI

а так же интересно, что свободная группа + интерпретатор и сразу интерпретатор по сути представляю из себя два изоморфных способа писать интерпретаторы: начальный и финальный
Алгебраически, структуры представляются в виде свободных структур и факторов по ним. Т.е., любая группа, это фактор-группа свободной группы.
Категорно (и сильно более общО, чем классическое алгебраическое), есть такое понятие алгебры для монады (и ещё более общее понятие модуля над моноидом в моноидальной категории).
Скажем, рекомендую проделать упражнение и посмотреть, что такое будет алгебра над монадой List или над монадой свободных магм (рекомендую понять, что это такое). Ну и алгебры над монадой свободных групп (или коммутативных моноидов, абелевых групп) тоже рекомендую посмотреть.
https://bartoszmilewski.com/2017/03/14/algebras-for-monads/
Есть забавная теоремка (у Маклейна точно должна быть), что монада полностью определяется своими алгебрами.
Можно брать и другие примеры алгебр для монады, навроде алгебр для монады свободных компактных хаусдорфовых топологических пространств.
Я думаю, что достаточно несколько (необязательно сложных!) примеров разобрать и идея будет понятна.
#article
Категорно (и сильно более общО, чем классическое алгебраическое), есть такое понятие алгебры для монады (и ещё более общее понятие модуля над моноидом в моноидальной категории).
Скажем, рекомендую проделать упражнение и посмотреть, что такое будет алгебра над монадой List или над монадой свободных магм (рекомендую понять, что это такое). Ну и алгебры над монадой свободных групп (или коммутативных моноидов, абелевых групп) тоже рекомендую посмотреть.
https://bartoszmilewski.com/2017/03/14/algebras-for-monads/
Есть забавная теоремка (у Маклейна точно должна быть), что монада полностью определяется своими алгебрами.
Можно брать и другие примеры алгебр для монады, навроде алгебр для монады свободных компактных хаусдорфовых топологических пространств.
Я думаю, что достаточно несколько (необязательно сложных!) примеров разобрать и идея будет понятна.
#article
NI
и никак не могу понять полезность обращения к lazyness, вроде G -> (forgetful) F -> (interpreter) G вполне достаточно
Насколько я понял, "ленивость" тут просто метафора, не имеющая ничего общего с ленивым порядком исполнения.
к
да, речь была про то, что вместо полезного вычисления мы оставляем дырку-конструктор, а сворачиваем всю структуру позже, добавляя отношения