AT
похоже, действительно, на “product of morphisms”
у Милевского это называется factorizer: https://bartoszmilewski.com/2015/01/07/products-and-coproducts/
(а форком зовет Jeremy Gibbons в Calculating Functional Programs)
Size: a a a
2018 May 25
AT
спасибо всем, кто откликнулся
Oℕ
у Милевского это называется factorizer: https://bartoszmilewski.com/2015/01/07/products-and-coproducts/
(а форком зовет Jeremy Gibbons в Calculating Functional Programs)
(а форком зовет Jeremy Gibbons в Calculating Functional Programs)
странное название
Oℕ
для меня factorizer звучит как что-то, что должно раскладывать на множители
AT
согласен; у нас в проекте это зовется `fsplice`и шеф попросил категорное название подобрать
DM
для меня factorizer звучит как что-то, что должно раскладывать на множители
ну вродь того и происходит
функция выделяет фактор (один правда)
функция выделяет фактор (один правда)
Oℕ
ну вродь того и происходит
функция выделяет фактор (один правда)
функция выделяет фактор (один правда)
?
DM
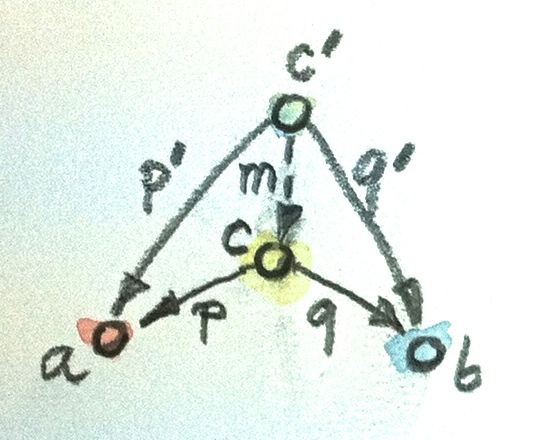
в статье функция записана как
fork :: (x -> a) -> (x -> b) -> (x -> (a, b))т.е. с намеком на получение не произведения а функции из некоего объекта в произведение (та самая факторизующая функция)
NI
Мне кажется, это просто декартово произведение
Это произведение двух морфизмов, да.
ЗП
ЗП
в стрелках так называется
Oℕ
истинно категорное имя
Oℕ
в стрелках так называется
по-моему называется оно то ли &&& то ли ***, а fanout просто в комментах написано
ЗП
AG
у Милевского это называется factorizer: https://bartoszmilewski.com/2015/01/07/products-and-coproducts/
(а форком зовет Jeremy Gibbons в Calculating Functional Programs)
(а форком зовет Jeremy Gibbons в Calculating Functional Programs)
у него и для копроизведений потом тоже
factorizer :: (a -> c) -> (b -> c) -> Either a b -> cЗП
factor и cofactor :D
Oℕ
у него и для копроизведений потом тоже
factorizer :: (a -> c) -> (b -> c) -> Either a b -> cну эт ваще
Oℕ
если бы я как-то и переименовал coproduct, то в какой-нибудь patternMatch
λ
Он же там через factorizer объясняет universal construction.
Что product это то, что нельзя _разложить_ через этот морфизм. Хотя это вроде оч нестрогое объяснение
Что product это то, что нельзя _разложить_ через этот морфизм. Хотя это вроде оч нестрогое объяснение