KV
Size: a a a
2018 November 28
Ты можешь моделировать стейт как отдельный объект
Ну то есть моделировать нечистые функции чистыми
NI
Ну то есть моделировать нечистые функции чистыми
Но есть нюанс — для моделирования "ресурсов" уже надо извращаться с продолжательным.
AG
Nikolay
Но не нарушится ли тогда свойство ассоциативности ? У нас же должно быть( f*g)*h= f*(g*h). Если у нас меняется глобальный стэйт , что часто в императивных языках , то легко сломать ассоциативность. Например при вызове g взводится глобальная переменная в true, а при вычислении f смотрим на эту переменную
в общем случае да, это https://ncatlab.org/nlab/show/duploid
Oℕ
Ну то есть моделировать нечистые функции чистыми
Моделировать нечистые функции морфизмами.
Обычное декартово замыкание в каких-то случаях может превратиться в какое-то более общее моноидальное.
Обычное декартово замыкание в каких-то случаях может превратиться в какое-то более общее моноидальное.
Oℕ
Я прошу прощения, что написал там x
Oℕ
Давайте вот так напишем
(A (х) State) -> (B (х) State)
(A (х) State) -> (B (х) State)
NI
Моделировать нечистые функции морфизмами.
Обычное декартово замыкание в каких-то случаях может превратиться в какое-то более общее моноидальное.
Обычное декартово замыкание в каких-то случаях может превратиться в какое-то более общее моноидальное.
На самом деле, вообще всё можно продолжениями записать.
Но на мой взгляд, почти всё такое выглядит неестественно ;-)
Но на мой взгляд, почти всё такое выглядит неестественно ;-)
2018 November 29
E
Привет, товарищи. Никто не может подкинуть пример категории, в которой есть морфизм, не представляющийся в виде композиции эпи- и мономорфизмов? А то вообще что-то ничего в голову не приходит, поскольку это свойство хорошо выполняется во многих конкретных категориях и во всех абелевых.
NI
https://ncatlab.org/nlab/show/regular+epimorphism
https://ncatlab.org/nlab/show/regular+monomorphism
Каждый мономорфизм, который
является регулярным эпиморфизмом и
каждый эпиморфизм, который
является регулярным мономорфизмом,
обязательно будет изоморфизмом.
https://ncatlab.org/nlab/show/regular+monomorphism
Каждый мономорфизм, который
является регулярным эпиморфизмом и
каждый эпиморфизм, который
является регулярным мономорфизмом,
обязательно будет изоморфизмом.
NI
Привет, товарищи. Никто не может подкинуть пример категории, в которой есть морфизм, не представляющийся в виде композиции эпи- и мономорфизмов? А то вообще что-то ничего в голову не приходит, поскольку это свойство хорошо выполняется во многих конкретных категориях и во всех абелевых.
Ой. Извиняюсь...
Спросонья, что ли, ответил не на тот вопрос ;-)
Спросонья, что ли, ответил не на тот вопрос ;-)
NM
В другом чате раньше вот так этот вопрос обсуждали.
NM
Мне кажется, просто придумать категорию "как граф". Кажется, я уже не первый раз это советую, да?)
Может быть удастся придумать, чтобы вообще не было мономорфизмов и эпиморфизмов, или чтобы их было как можно меньше.
Может быть удастся придумать, чтобы вообще не было мономорфизмов и эпиморфизмов, или чтобы их было как можно меньше.
NM
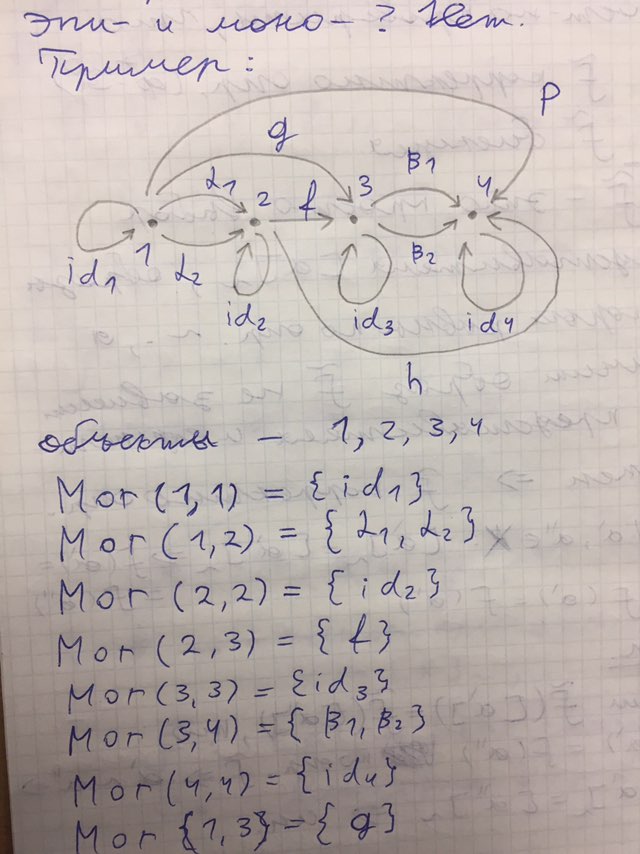
Ну я использовал категорию из 4 объектов с хитрым расположением стрелок, так чтобы сломать для морфизма в центре эпи- и моно-
Oℕ
Фух, я чуть не начал спорить с Ником
Oℕ
Мне кажется, просто придумать категорию "как граф". Кажется, я уже не первый раз это советую, да?)
Может быть удастся придумать, чтобы вообще не было мономорфизмов и эпиморфизмов, или чтобы их было как можно меньше.
Может быть удастся придумать, чтобы вообще не было мономорфизмов и эпиморфизмов, или чтобы их было как можно меньше.
Не очень понятно.
"Как граф" - это свободная категория?
Или со специальной таблицей "умножения" морфизмов?
"Как граф" - это свободная категория?
Или со специальной таблицей "умножения" морфизмов?
NM
Со специальной таблицей умножения. Просто несколько стрелок нарисовать, придумать к ним правила умножения. Главное жадничать — чем меньше стрелок нарисуешь, тем проще жить.
E
Мне кажется, просто придумать категорию "как граф". Кажется, я уже не первый раз это советую, да?)
Может быть удастся придумать, чтобы вообще не было мономорфизмов и эпиморфизмов, или чтобы их было как можно меньше.
Может быть удастся придумать, чтобы вообще не было мономорфизмов и эпиморфизмов, или чтобы их было как можно меньше.
У меня уже получилось построить хороший граф, благодарю )
E
У меня получилось вот так
E
Со специальной таблицей умножения. Просто несколько стрелок нарисовать, придумать к ним правила умножения. Главное жадничать — чем меньше стрелок нарисуешь, тем проще жить.