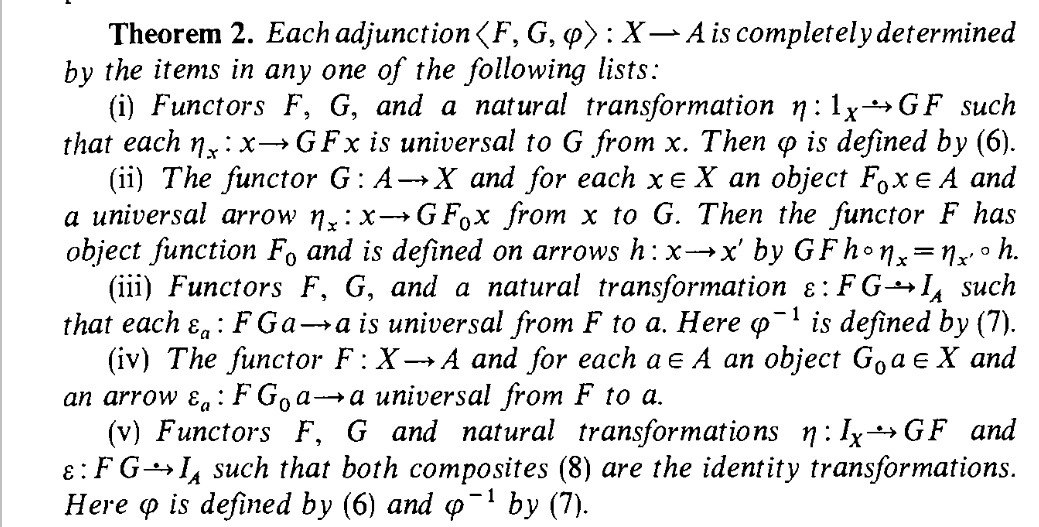Идея, видимо, основная была как раз в том, чтобы все морфизмы относительно общего расположения объектов били только в одну сторону

Такоэ вот ещё —
Теория категорий
Александр Лузгарев
http://mahalex.net/special-courses/_cats/cats.pdf

А может ли ещё кто-то прояснить ситуацию с представимостью забывающих функторов?

Как я понял, мы определяем степенной функтор как фиксирование одного объекта категории и сопоставление любому объекту той категории множества морфизмов в ней из фиксированного объекта в произвольный. Перевод морфизмов очевиден.
Функтор определяем как представимый, если он является степенным, т.е. есть такой фиксированный объект, по которому он восстанавливается как степенной.
Тогда простейший пример представимого функтора - забывающий из категории групп в категорию множеств. Он представим аддитивной группой целых чисел.
Забывающий функтор вкладывает морфизмы между объектами данной категории в морфизмы между ними в категории множеств. Разберёмся с ним в случае с группами.
Берём морфизмы из Z в произвольную группу G и и сопоставляем им гомоморфизм f_g : 1 -> g (единица является порождающей в Z, а ноль переходит в единицу группы). По нему мы однозначно восстанавливаем g^2, g^-1 и так далее.
Вот тут я не совсем понял. Мы ведь совсем не утверждаем, что так мы восстановим все элементы группы. Мы ведь просто предложили такую конструкцию как биекцию или что?

Он не отображает объекты в множества морфизмов между ними, это не просто функтор Hom. Это забывающий функтор из произвольной категории C, вида F: C\rightarrow Set, который имеет очевидный изоморфизм с ковариантным функтором Hom(1, ), где 1 — представляющий объект категории C. Представляющий объект можно получить, рассмотрев левый сопряженный функтор U к F, такой, что U: Set\rightarrow C, то F представим U(1), где 1 — синглетон в Set, т.к. Hom(U(1),X) = Hom(1,F(X)) = F(X). Число морфизмов из представляющего объекта в категории C в интересующий нас объект X — образ действия представимого забывающего функтора F (так как в Set все объекты изоморфны с точностью до мощности).

А морфизмы из C под действием функтора переходят в какие-то функции в Set, которые могут быть построены между множествами морфизмов Hom(1,F(X)) и Hom(1,F(Y)), например, то есть, любых двух объектов изначальной категории.

Например порождающий объект в Grp — Z, так как это свободная группа порожденная синглетоном

Ну или в Top порождающий объект — одноточечное пространство

Я сопряженные функторы не шарю, если что

Тогда не понимаю, как тут забывчивость приплетается

Т.е. нужно, грубо говоря, показать, что забывающий функтор ведёт себя как степенной

По сути, Hom(U(1),X) = Hom(1,F(X))  — определение сопряженности функторов U и F

Просто в курсе Шабата не было про изоморфность функторов, поэтому достаточно показать, что он ведёт себя так

Кроме как через изоморфизм, вроде никак нельзя

Ну он для групп показал, что любому морфизму из Z в произвольную группу G можно сопоставить отображение 1 -> g, где g - элемент группы

Но я не понял прикола дальше с тем, что по нему однозначно восстанавливаются все степени g, дескать что это нам вообще даёт

ну это функтор Hom(1,g)

Куча опредений

Недавно обсуждали. Можно через юнит и коюнит, можно через универсальные морфизмы и из и в

это Маклейн 83