AG
Size: a a a
2018 March 11
категория с одним объектом
λ
есть случаи когда морфизмы между двумя объектами различимы, а когда нет
еще раз отправлю к эпи и мономорфизмам
еще раз отправлю к эпи и мономорфизмам
мне кажется это контекстно
в общем случае они просто различимы
в общем случае они просто различимы
DM
да, но сомнения (по своему же опыту) вызывает то, что делать с этим
как их различать кроме как по буковкам, если все что есть это объекты (как кажется по началу)
как их различать кроме как по буковкам, если все что есть это объекты (как кажется по началу)
λ
да, но сомнения (по своему же опыту) вызывает то, что делать с этим
как их различать кроме как по буковкам, если все что есть это объекты (как кажется по началу)
как их различать кроме как по буковкам, если все что есть это объекты (как кажется по началу)
я это чувство победил концентрацией на стрелках, объектов нет (кстати некоторые авторы так и говорят) а есть только стрелки
λ
все объекты однозначно задаются стрелками (пеньки единичными например)
DM
это ортогонально имхо
к
но ведь в определении стрелки тоже есть объекты
DM
ну может под углом, но не прям связано
к
то есть как не имея объектов задать
A -> B
?
A -> B
?
к
я это чувство победил концентрацией на стрелках, объектов нет (кстати некоторые авторы так и говорят) а есть только стрелки
единичные стрелки или стрелки из инициального объекта?
λ
ну можно сказать что у стрелок есть концы) ну я не предлагаю отказаться от объектов, просто надо сместить фокус на стрелки
DM
Шерзод написал уже
некоторые не задают категорию с объектами, вместо объекта может быть идентити морфизм
некоторые не задают категорию с объектами, вместо объекта может быть идентити морфизм
к
мне очень давно не нравится, как в теоркате функтор отображает и объекты, и морфизмы
типа
то есть
в принципе если представить, что в
при этом
то можно каждый объект
и тогда у функтора можно оставить только одно определение отображения морфизмов, а именно
но это какое-то слишком строгое ограничение
типа
A, B : C
f : A -> B
F : C -> D
F(A) : D
F(B) : D
F(f) : F(A) -> F(B)
то есть
F ведет себя для объектов и морфизмов по-разномув принципе если представить, что в
C и D есть начальные объекты I_C и I_Dпри этом
F(I_C) = I_Dто можно каждый объект
C представить как морфизм I_C ->A, I_C -> Bи тогда у функтора можно оставить только одно определение отображения морфизмов, а именно
F(I_C -> A) : D = I_D -> F(A) : Dно это какое-то слишком строгое ограничение
DM
я не понял, что значит "ведет себя по-разному"
функтор все что делает, это задает соответствие между двумя категориями
функтор все что делает, это задает соответствие между двумя категориями
DM
для этого надо замапить объекты и морфизмы, так чтобы первоначальная структура была верна
к
тут смотри какое дело, мой строго типизованный мозг не может принять тот факт, что F принимает и объекты, и стрелки, и отдает при этом тоже объекты или стрелки
λ
ну да, тут проглядывает теоретико-множественный взгляд, там ведь функции и они всё делают "одинаково"
но в категориях есть структура, поэтому функторы более "ограничены" в некотором смысле, чем функции, они должны не просто отображать содержимое категории, но и сохранить её структуру
но в категориях есть структура, поэтому функторы более "ограничены" в некотором смысле, чем функции, они должны не просто отображать содержимое категории, но и сохранить её структуру
λ
мне очень давно не нравится, как в теоркате функтор отображает и объекты, и морфизмы
типа
то есть
в принципе если представить, что в
при этом
то можно каждый объект
и тогда у функтора можно оставить только одно определение отображения морфизмов, а именно
но это какое-то слишком строгое ограничение
типа
A, B : C
f : A -> B
F : C -> D
F(A) : D
F(B) : D
F(f) : F(A) -> F(B)
то есть
F ведет себя для объектов и морфизмов по-разномув принципе если представить, что в
C и D есть начальные объекты I_C и I_Dпри этом
F(I_C) = I_Dто можно каждый объект
C представить как морфизм I_C ->A, I_C -> Bи тогда у функтора можно оставить только одно определение отображения морфизмов, а именно
F(I_C -> A) : D = I_D -> F(A) : Dно это какое-то слишком строгое ограничение
initial и terminal объекты есть не всегда
Oℕ
окей, вот этот момент мне пока не понятен был
всегда считал что интересует только факт наличия стрелки между двумя объектами, а две стрелки между двумя одинаковыми парами объектаов являются одной и той же стрелкой на уровне теоркатка
всегда считал что интересует только факт наличия стрелки между двумя объектами, а две стрелки между двумя одинаковыми парами объектаов являются одной и той же стрелкой на уровне теоркатка
легко можно проверить себя
Если на важен только факт, то вот такое понятие
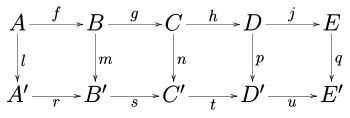
https://en.m.wikipedia.org/wiki/Commutative_diagram
Или такое https://ncatlab.org/nlab/show/locally+small+category
Теряют смысл
Если на важен только факт, то вот такое понятие
https://en.m.wikipedia.org/wiki/Commutative_diagram
Или такое https://ncatlab.org/nlab/show/locally+small+category
Теряют смысл
DM
в категорном смысле функтор делает ровно одну вещь =)
просто в другой модели это выражается более сложно, потому что не является столь естественным для нее
просто в другой модели это выражается более сложно, потому что не является столь естественным для нее