ЗП
Size: a a a
2018 March 11
ATS мне кажется странным
NI
Зато можно в монады на stm32! ;-)
ЗП
В плане?)
ЗП
Да и на агде я видел более правильно сделанные категории
NI
В плане, что ATS годится для совсем низкоуровневого программирования.
На нём и драйвера линуксовые писали (не знаю, были там в коде монады.....) и чотта про ардуинки видел.
На нём и драйвера линуксовые писали (не знаю, были там в коде монады.....) и чотта про ардуинки видел.
Oℕ
What is missing in ATS right now is the ability to synthesize an argument according to the type
тупеклассов/имплиситов не завезли
тупеклассов/имплиситов не завезли
NI
Но делают ATS3!!
;-) Ладно, хватит уже...
;-) Ладно, хватит уже...
AV
о, интересное обсуждают
OP
кто читает концептуальную математику
KV
кто читает концептуальную математику
Я бы читал, будь у меня второе издание
OP
на стр. 127 (Brouwer 's theorems) сказано такое
> none of E, C, S, is a retract of any of I, D, B.
> none of E, C, S, is a retract of any of I, D, B.
OP
почему?
в случае, где E - множество из двух точек, I - отрезок, можно найти отображения
скажем, s отображает точки в концы отрезка, r отображает левую половину в первую точку, середину в первую точку, правую половину во вторую точку
в случае, где E - множество из двух точек, I - отрезок, можно найти отображения
s :: E -> I и r :: I -> E, r . s = id Eскажем, s отображает точки в концы отрезка, r отображает левую половину в первую точку, середину в первую точку, правую половину во вторую точку
KV
почему?
в случае, где E - множество из двух точек, I - отрезок, можно найти отображения
скажем, s отображает точки в концы отрезка, r отображает левую половину в первую точку, середину в первую точку, правую половину во вторую точку
в случае, где E - множество из двух точек, I - отрезок, можно найти отображения
s :: E -> I и r :: I -> E, r . s = id Eскажем, s отображает точки в концы отрезка, r отображает левую половину в первую точку, середину в первую точку, правую половину во вторую точку
Речь же про непрерывные функции.
r здесь не будет непрерывной, непрерывно только в один из концов можно стянуть.OP
Речь же про непрерывные функции.
r здесь не будет непрерывной, непрерывно только в один из концов можно стянуть.в определении retract нет непрерывности
т.е. там должно быть сказано что-то вроде "невозможно построить непрерывные ретракции"?
т.е. там должно быть сказано что-то вроде "невозможно построить непрерывные ретракции"?
KV
в определении retract нет непрерывности
т.е. там должно быть сказано что-то вроде "невозможно построить непрерывные ретракции"?
т.е. там должно быть сказано что-то вроде "невозможно построить непрерывные ретракции"?
Технически, да, надо было уточнить. Но это вроде бы понятно из контекста, в формулировках теорем Брауэра там только непрерывные ретракции, ну и вообще весь раздел про непрерывное
OP
спасибо
OP
там ещё чуть выше упражнение 2 сложное
OP

Вот так я понимаю гипотезу
OP
нам нужно доказать, что
forall g :: A -> A exists a :: T -> A :g . a = aOP
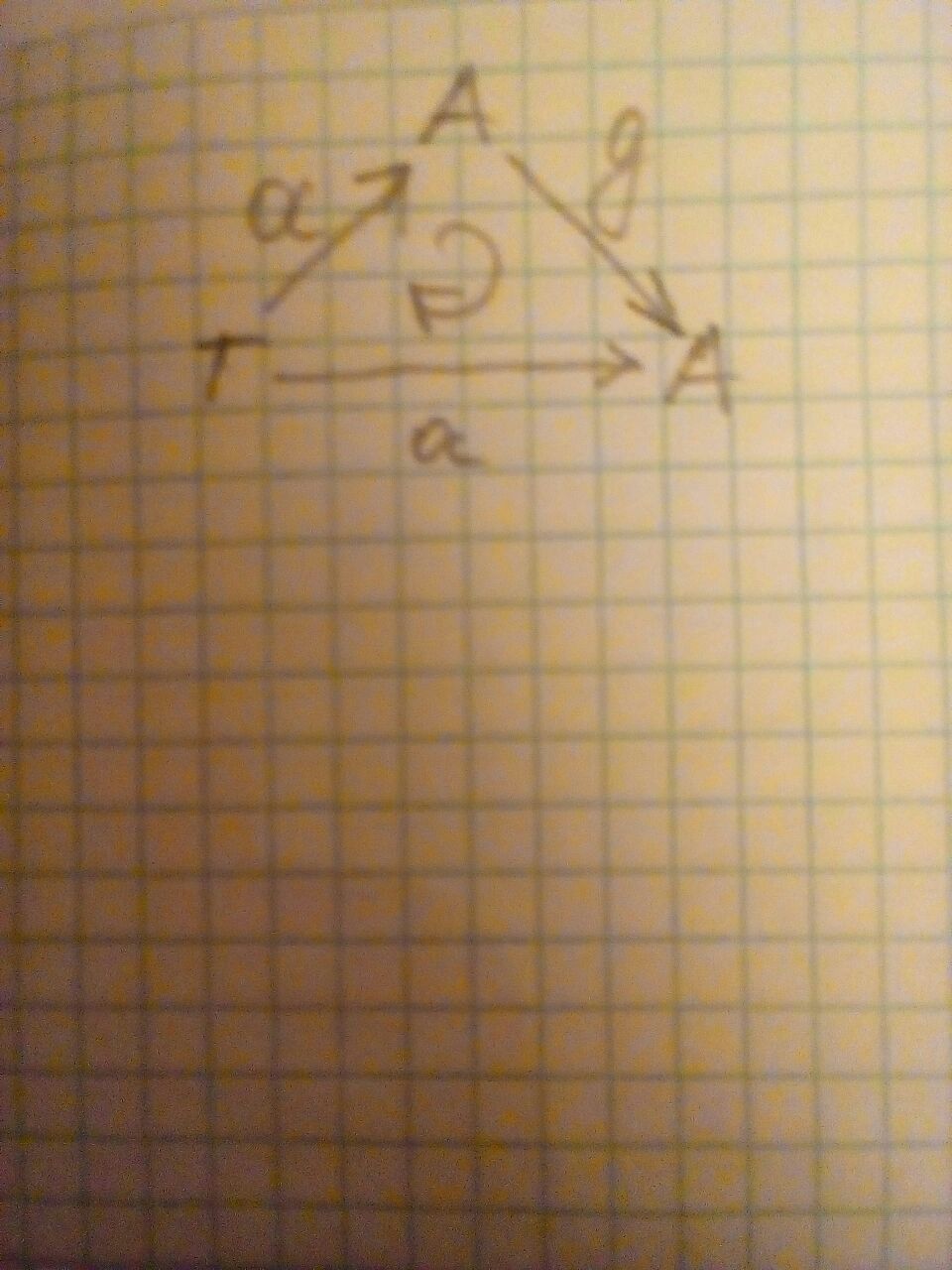
Т.е. вот так



