Size: a a a
2018 April 01

А лекция на закрытии Московской математической олимпиады: http://olympiads.mccme.ru/mmo/2018/zakr.htm
2018 April 02

Решение задачи 302.
#решение
#решение

303. Точка M – середина стороны BC треугольника ABC. Из вершины С опущен перпендикуляр CL на прямую AM (L лежит между А и М). На отрезке AM отмечена точка K так, что AK = 2LM. Докажите, что ∠BKM = ∠CAM.
#задача
#задача

Александр Хачатурян предлагает очень красивый геометрический подход к тригонометрии. Рекомендую его лекцию всем учителям, а также тем, кто запутался в тригонометрии:
#урок
#урок
2018 April 03

Доступна видеозапись лекции В.Ю.Протасова «Теорема Понселе — яркая и загадочная (Как одна задача элементарной геометрии вот уже два века не дает покоя профессиональным математикам)»
2018 April 06

M point divides the BC side of the ABC triangle in two. A perpendicular line CL starts from vertex C and falls onto AM leg (with L situated between A and M). Leg AM hosts K point with AK = 2LM.
You are to prove that ∠BKM = ∠CAM
You are to prove that ∠BKM = ∠CAM
2018 April 08

И снова самореклама. Мы делаем новую летнюю школу для программистов: univer-sum.ru
Расскажите о нас своим друзьям-школьникам, которые хотят научиться программировать.
Расскажите о нас своим друзьям-школьникам, которые хотят научиться программировать.
2018 April 09

Константин Кноп опубликовал ссылки на пособия по геометрии: https://m.facebook.com/groups/316171858533757?view=permalink&id=1009219972562272
2018 April 10

Александр Шкловер рассказал, как встроить курс логики в курс планиметрии 7 класса, чтобы ученики освоили новые логические понятия на знакомом материале: https://youtu.be/BSdPylw6fpQ
#урок #вертикаль
#урок #вертикаль
2018 April 11
2018 April 14

В знак того, что я не собираюсь никуда переходить из Телеграма, список всех моих публичных каналов:
@geometrykanal
@mylunchbox
@childrenmath
@univer_sum_news
@oneprep
@sch_int
@natanet
@geometrykanal
@mylunchbox
@childrenmath
@univer_sum_news
@oneprep
@sch_int
@natanet
2018 April 15

Константин Кноп продолжает выкладывать хорошие книги:
И. Кушнир. Альтернативные способы решения задач. Геометрия.
И. Кушнир. Избранные задачи по геометрии. Трапеция.
И. Кушнир. Геометрия. Поиск и вдохновение. Геометрия на баррикадах.
И. Кушнир. Шедевры школьной математики. Книга 1.
И. Кушнир. Шедевры школьной математики. Книга 2.
И. Кушнир. Векторные методы решения задач.
И. Кушнир. Геометрические воспоминания.
И. Кушнир. Атлас кубических пирамид.
Е.Н и Н.М. Рогановские, О.И.Тавгень. Факультативные пособия по геометрии.
С.Э.Нохрин Базовые конструкции планиметрии.часть1 часть 2
И. Кушнир. Альтернативные способы решения задач. Геометрия.
И. Кушнир. Избранные задачи по геометрии. Трапеция.
И. Кушнир. Геометрия. Поиск и вдохновение. Геометрия на баррикадах.
И. Кушнир. Шедевры школьной математики. Книга 1.
И. Кушнир. Шедевры школьной математики. Книга 2.
И. Кушнир. Векторные методы решения задач.
И. Кушнир. Геометрические воспоминания.
И. Кушнир. Атлас кубических пирамид.
Е.Н и Н.М. Рогановские, О.И.Тавгень. Факультативные пособия по геометрии.
С.Э.Нохрин Базовые конструкции планиметрии.часть1 часть 2
2018 April 16

И еще одна коллекция геометрических книг: http://eek.diary.ru/p86841314.htm
2018 April 17

условия проходившей в воскресенье устной олимпиады по геометрии
2018 April 18

Продолжая тригонометрическую тему, Константин Кноп выложил свои заметки о рациональной тригонометрии. Это его попытка начать обзор идей Нормана Уайлдбергера: https://www.facebook.com/groups/matkruzhki/1013683662115903/
2018 April 21

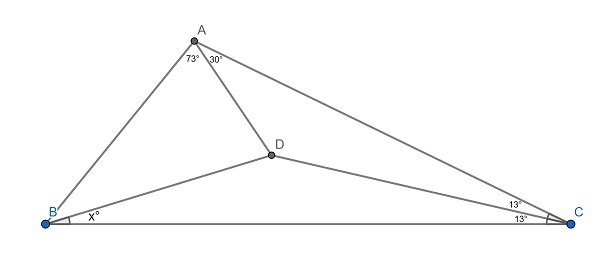
Анатолий Воробей предлагает решить задачу про углы (несколько углов дано, найдите угол x)
2018 April 22


Доказать, что радиус серенького круга равен 1/5 радиуса синего.
#сангаку
#сангаку

История и решение:
http://telegra.ph/Zadacha-pro-ugly-04-20
http://telegra.ph/Zadacha-pro-ugly-04-20
2018 April 23

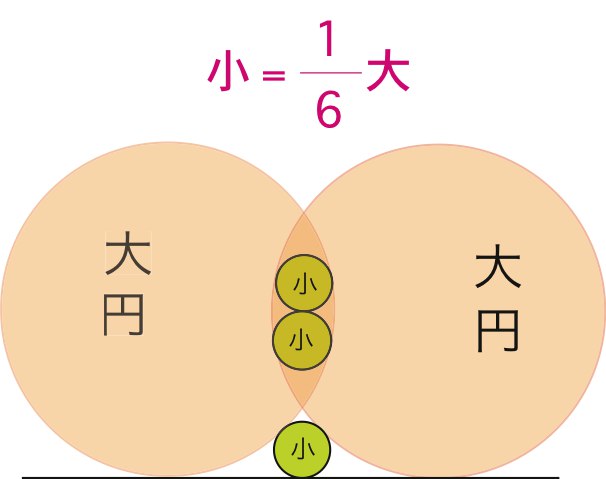
Доказать, что радиусы маленьких кругов равны 1/6 радиуса больших кругов.
#сангаку
#сангаку