342. Правильный тетраэдр и правильную четырёхугольную пирамиду, все рёбра которых равны, склеили равными треугольными гранями. Сколько граней у получившегося многогранника?

#задача

343. Правильный тетраэдр вписан в шар. На его гранях построены правильные прямоугольные пирамиды. Сколько граней у получившегося многогранника?

#задача

#Challenge A Gardener is going to put a triangle shaped piece of grass into a congruent triangle shaped land but he finds out that the land is not in the same direction with grass piece and it's reflected! He can not put the grass in there upside-down (who wants a piece of soil and some roots in it instead of a green shiny grass!). But suddenly he comes up with a great idea! He cuts the grass into 3 pieces and puts those together with some rotation in the land. Can you say how he is going to do that?

If you are not interested in the story(!) the problem wants you to cut a triangle into 3 pieces and put them together again without reversing pieces (just rotation and translation is allowed) to form a triangle congruent to the first one which is reversed (reflected).

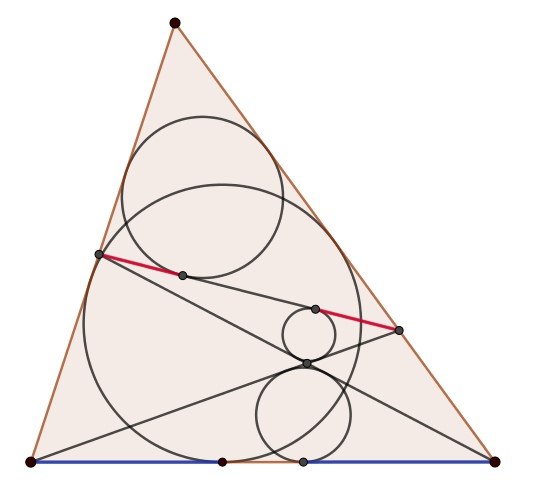
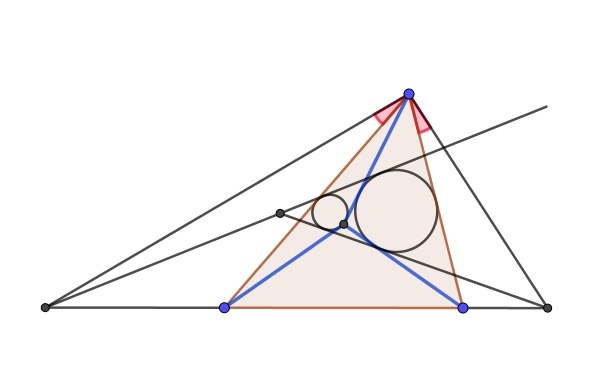
Краткосрочный курс повышения квалификации преподавателей «Некоторые
переломные моменты в развитии геометрии»

Лекции:
02.06 вторник, 10:00 – 12:00
03.06 среда, 10:00 – 12:00
05.06 пятница, 10:00 – 12:00
08.06 понедельник, 10:00 – 12:00
09.06 вторник, 10:00 – 12:00
Семинары: по запросу участников, время согласно договоренности.

Преподаватель: Тиморин Владлен Анатольевич, д.ф.-м.н., PhD,
https://www.hse.ru/staff/vtimorin.

По итогам курса выдаются удостоверения о повышении квалификации установленного образца. Курс предлагается бесплатно в рамках деятельности Международного Научно-Методического Центра (МНМЦ) НИУ ВШЭ

Записаться на курс: https://mnmc.hse.ru/contact

Подробности: https://math.hse.ru/turnpoints_geom_vt
Там, правда, пишут, что это для преподавателей вузов и аспирантов, но на самом деле можно не только им.

Новая задача: доказать, что синие отрезки равны тогда и только тогда, когда равны красные.

344. Можно ли расположить в пространстве 13 одинаковых шариков так, чтобы они не пересекались и при этом 12 шариков касались одного.

#задача

По следам задачи 344

Посмотрите видео https://www.etudes.ru/ru/etudes/contact-number/
Там есть и решение, и история этой задачи.

Почитайте статью https://nplus1.ru/material/2016/04/07/spheres

И приходите послушать Виктора Клепцына:

В воскресенье 7 июня в 18:30 Виктор Клепцын (научный сотрудник CNRS, Университет Ренна) прочтёт лекцию «Решётки и упаковки шаров».

Лекция будет читаться через zoom. Подробные инструкции будут опубликованы в новостях курса (их получат те, кто запишется на курс).
Анонс лекции:  https://compsciclub.ru/courses/csseminar/2020-spring/classes/5816/

картинка по выходным: разрезание правильного треугольника на 15 равных частей от П.Гузенко (и есть похожее на 30 частей)

напомним еще найденное несколько лет назад М.Патракеевым удивительное разрезание правильного трегуольника на 5 равных частей, https://t.me/cme_channel/422

и все, больше не известно почти ничего: например, никто не знает, можно ли разрезать правильный треугольник на 7 или 11 равных частей (хотя некоторые экзотические примеры есть — видимо самый простой — разрезание https://t.me/cme_channel/1027 на 10935 равных треугольников)

если уж начал делить правильный треугольник на равные части — трудно остановиться
// via https://www.facebook.com/groups/mathpuz/

(напомним, что значит равенство частей, когда они несвязные: если считать, что каждый цвет напечатан на своем прозрачном листе, то любые два листа можно совместить так, чтобы части совпали)

Источник: https://vk.com/wall-158730626_193

Профессор НИУ ВШЭ Владлен Тиморин читает курс «Некоторые переломные моменты в развитии геометрии».
Видеозаписи этих занятий собираются здесь: https://www.youtube.com/playlist?list=PLEI0cU52ctD5FeEuUxEKJkUnbn3Q0PeRk

Первые 4 видео (первые две лекции) будут понятны абсолютно всем.
Дальше — немного посложнее, для заинтересованных.

#видео

Всем привет! Вторничная гифка - одно из замечательных свойств точки Шалтая.

https://youtu.be/LTp6A5DT6S8

В. Клепцын. Решётки и упаковки шаров (появилась видеозапись)

«Понятно, как наиболее плотно расположить одинаковые монеты на плоском столе: их центры должны образовывать шестиугольную решетку. Впрочем, даже это не столь просто доказать строго — а в больших размерностях, конечно, задача становится невероятно сложной.

Тем не менее, в 2016 году Марина Вязовска доказала, что плотнейшая упаковка шаров в пространстве размерности 8 — замечательная решётка Коркина—Золотарёва, она же решётка E_8. (А о связи этой решётки с передачей информации я постараюсь сказать пару слов.) И почти сразу же — такой же результат она получила в соавторстве с Коном, Кумаром, Радченко и Миллером в размерности 24, где есть другая замечательная решётка — решетка Лича.

Я расскажу несколько первых шагов этих доказательств — показав, как такой результат в принципе может быть получен; ключевым элементом здесь будет теорема, одновременно доказанная в начале 2000-х Горбачёвым и Коном и Элкисом.»

Новая задача! Синие отрезки равны, доказать, что красные углы равны.

Всем привет! Наконец-то разбор задачи номер 8 со стены. Два способа посчитать и геометрическое решение, основанное на степени точки относительно точки... Есть еще одно геометрическое решение, но о нем я, быть может, напишу чуть позже...
https://m.vk.com/@olympgeom-razbor-zadachi-so-steny-8

Вторничная гифка! Центры вписанных и вневписанных окружностей треугольников ABC, BCD, CDA и DAB для вписанного четырехугольника ABCD.

Сколькими способами можно расположить несколько окружностей на плоскости?

https://youtu.be/bRIL9kMJJSc

#видео

345. На стороне CD квадрата ABCD построен внутрь равнобедеренный треугольник KCD с углом 15° при основании. Докажите, что ABK — правильный треугольник.

#задача