Решение задачи 45,  в общем-то, укладывается в рисунок. Ключевая идея в том, что точка E является центром еще одного прямоугольника, подобного двум данным. Причем сумма двух коэффициентов подобия равна 1. На рисунке показана и вторая копия одного из прямоугольников, симметричная первой относительно E.

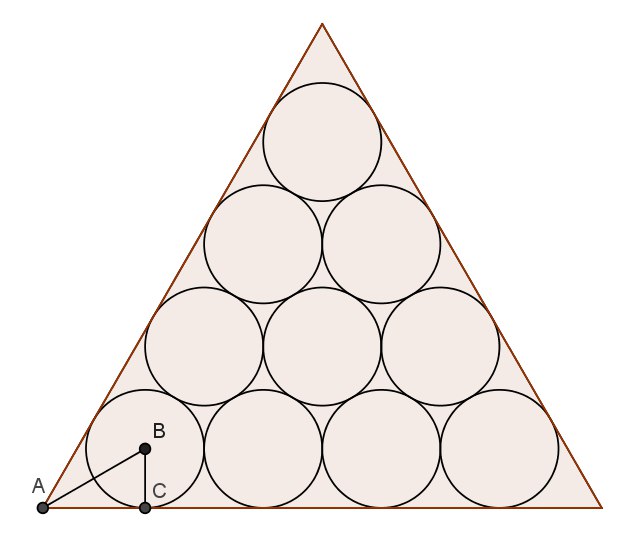
46. Десять одинаковых единичных окружностей расположены в форме , напоминающей правильный треугольник: 4 касающихся окружности в нижнем ряду, 3 в ряду над ними, 2 в следующем и 1 на вершине. Затем вся эта «пирамидка» вписана в настоящий правильный треугольник. Найдите его площадь.

Рисунок к задаче 46 (решение будет чуть позднее):

Ответ: 6(3+2sqrt(3)). Примерно 38.78. Дополнительно отметим, что площадь всех кругов внутри треугольника равна 10pi, то есть примерно 31.42. Иными словами, вне кругов почти 20% площади треугольника. А на первый взгляд и не скажешь!

Как получить ответ? На рисунке показан прямоугольный треугольник ABC. Его меньший катет — радиус окружности, то есть 1. Угол А равен 30°, поэтому гипотенуза треугольника равна 2, а значит, больший катет равен корню из 3. Сторона правильного треугольника состоит из шести радиусов и двух отрезков, равных AC, то есть равна 6+2sqrt(3). Зная это, уже очень просто вычислить его площадь.

Задача 47 взята мной из книги «Избранные задачи и теоремы элементарной математики. Геометрия. Планиметрия» Шклярский, Ченцов, Яглом:

Решение задачи 47:

48. Бумажный прямоугольный треугольник АВС перегнули по прямой так, что вершина С прямого угла совместилась с вершиной В и получился четырехугольник. В каких отношениях точка пересечения диагоналей четырехугольника делит эти диагонали?

Решение задачи 48

49. O — точка пересечения диагоналей в параллелограмме ABCD. Точка M лежит на продолжении стороны AB за точку B. Известно, что угол AMO равен углу ВAD. Докажите, что MC = MD.

Решение задачи 49

50.  Два квадрата (необязательно равные) пересекаются в восьми точках. Найдите пару равных и взаимно перпендикулярных отрезков.

Живой чертеж к задаче 50

51. В треугольнике ABC на сторонах AB, AC и BC выбраны точки D, E и F соответственно так, что BF = 2CF, CE = 2AE и угол DEF — прямой. Докажите, что DE — биссектриса угла ADF.

Решение задачи 51

52. Точка O — центр описанной окружности остроугольного треугольника ABC. Описанная окружность треугольника AOC вторично пересекает стороны AB и BC в точках E и F. Оказалось, что прямая EF делит площадь треугольника ABC пополам. Найдите угол B.

Решение задачи 52

53.  В выпуклом шестиугольнике ABCDEF все стороны равны и AD = BE = CF. Докажите, что в него можно вписать окружность (то есть внутри шестиугольника существует окружность, касающаяся всех его сторон).