Этой картинкой мы открываем новый жанр нашего канала: доказательства без слов и разнообразные картинки по математике. Одна картинка в день: 100 дней, 100 картинок, 100 фактов, 100 доказательств без слов. Смотрите!

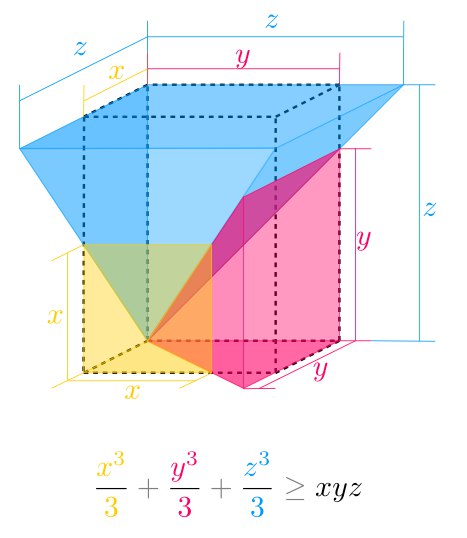
#картинка

Тест для 8 класса. Четырехугольники

#тест

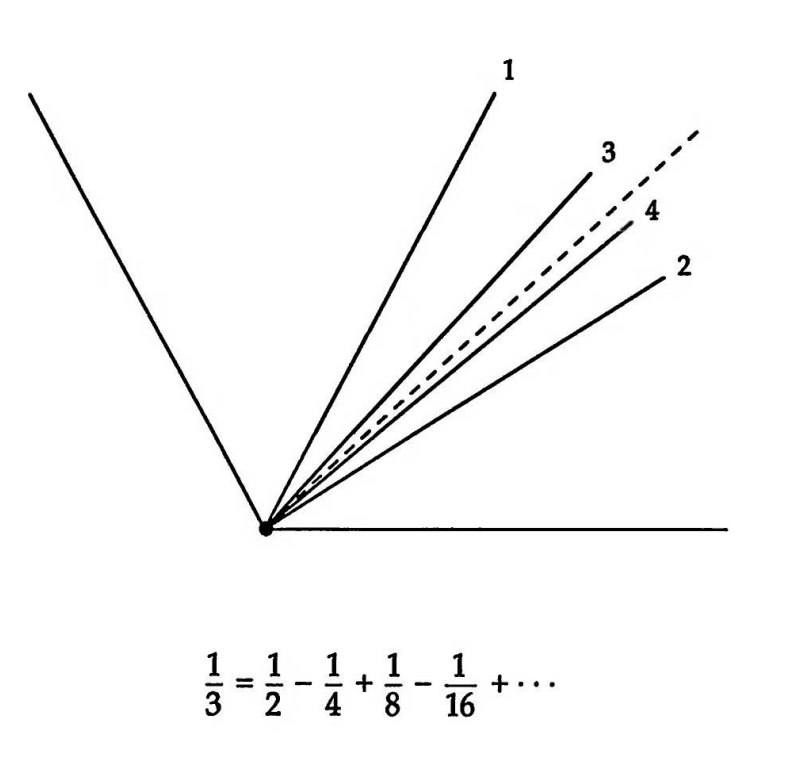
Картинка 2. Трисекция угла за бесконечное число шагов.

#картинка

88. Серединные перпендикуляры к сторонам AB и AC треугольника ABC пересекают высоту, проведённую к стороне BC, в точках K и M. Найдите радиус окружности, описанной около треугольника ABC, если AK=a, AM=b.
#задача

Решение задачи 87.

#решение

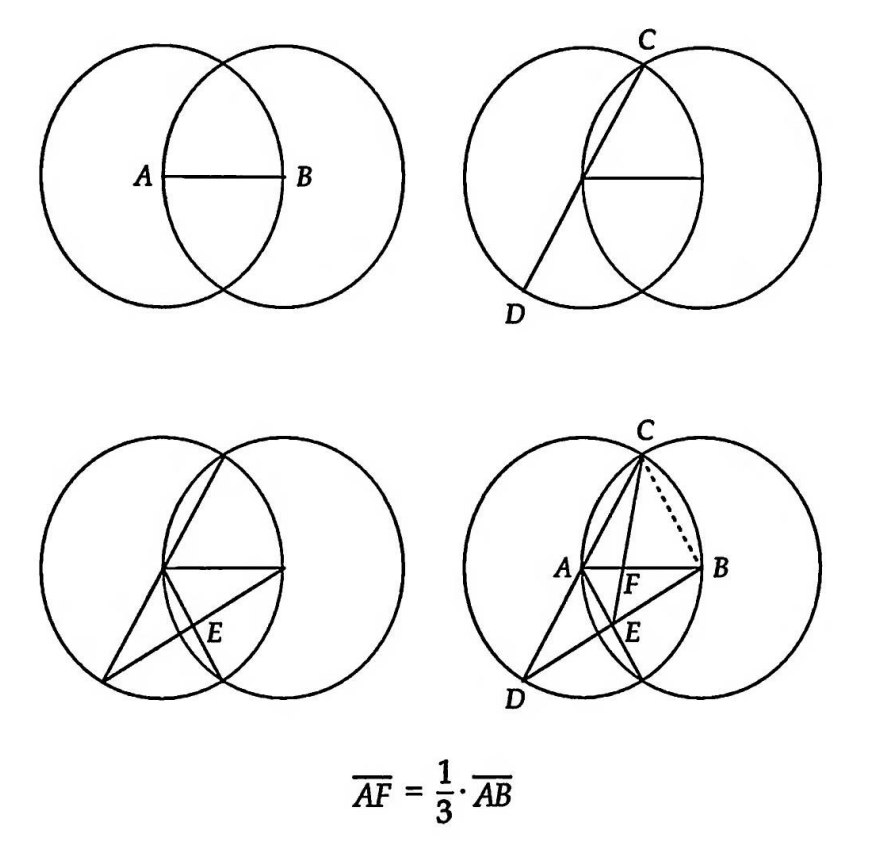
Картинка 3. Трисекция отрезка
#картинка

89. Около окружности описана равнобокая трапеция. Боковая сторона трапеции равна a, отрезок, соединяющий точки касания боковых сторон с окружностью, равен b. Найдите диаметр окружности.
#задача

Решение задачи 88.

#решение

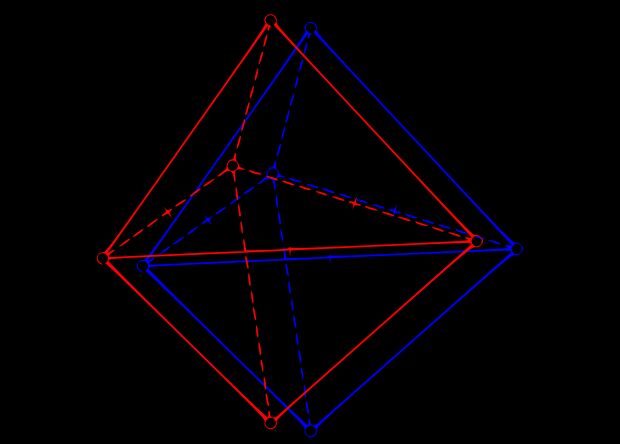
Задача Данцера и Грюнбаума формулируется просто — какое наибольшее число точек в пространстве можно поместить так, чтобы любые три из них образовывали остроугольный треугольник.

На плоскости это число равно трем. Любая попытка поставить четвертую точку приведет к возникновению тупого угла. Для трехмерного пространства это число равно пяти. Для пространств высшей размерности такое число точно неизвестно.

Известно, что «острое множество» конечно для любой размерности — число точек в нем должно быть меньше числа вершин в кубе соответствующей размерности.

Десятиклассник московской школы 179, Дмитрий Захаров, улучшил предыдущую оценку, построив очень простой пример.

Предположим, что для размерности N мы можем построить «острое множество» из максимального количества точек. Покажем, как построить «острое множество» из в два раза большего количества точек для пространства размерности N+2. Для этого раздвоим каждую точку исходного множества. При этом все раздвоения сделаем немного отличающимися друг от друга в проекции на плоскость двух новых размерностей. Тогда, если величина смещения подобрана правильно, а это всегда можно сделать, новое множество тоже будет «острым».

Дискуссия в ФБ Арсения Акопяна
Работа Дмитрия Захарова
Текст со ссылками на предыдущие оценки

#новость

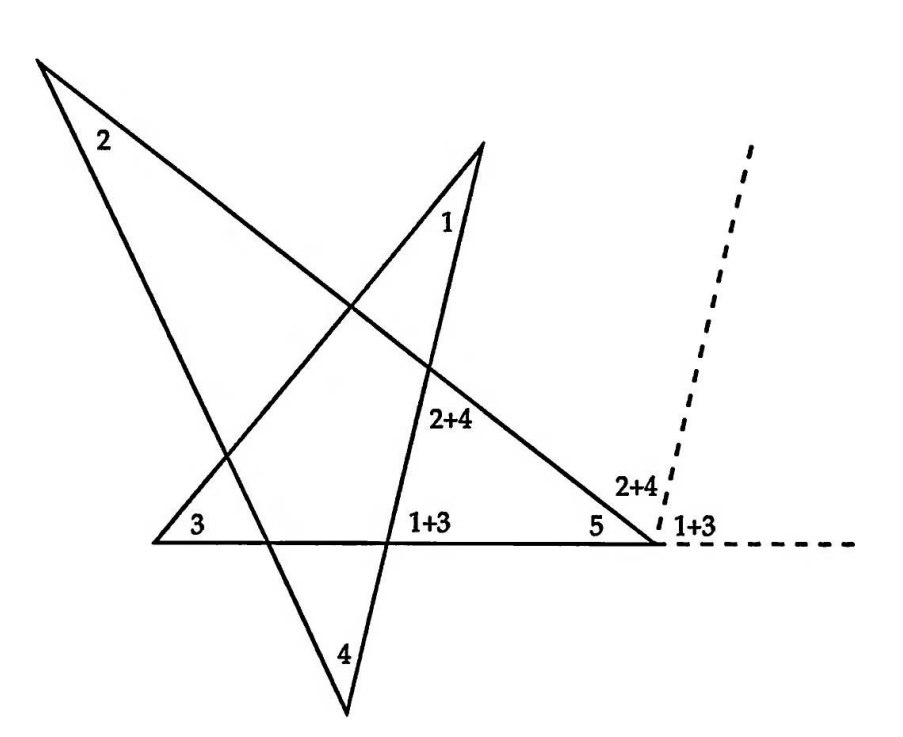
Картинка 4. Сумма углов пятиконечной звезды равна 180°.

#картинка

90. В окружности проведён диаметр AB. Другая окружность с центром в B пересекает первую в точках C и D; M — точка первой окружности внутри второй. Прямая AM пересекает вторую окружность в точках E и F (E лежит между A и F). Найдите MF, если MC=a, MD=b.

#задача

Решение задачи 89.

#решение

Решение задачи 90.

#решение

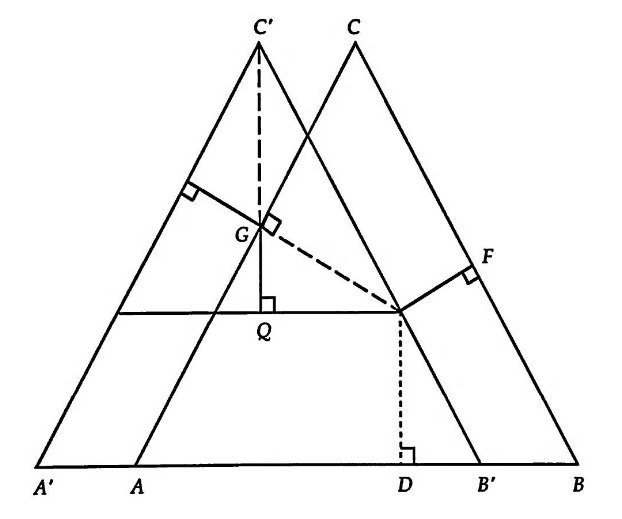
Картинка 5. Теорема Вивиани. Сумма расстояний от произвольной точки внутри или на стороне правильного треугольника равна высоте этого треугольника.

#картинка

Добавили более простой вариант решения задачи 90.

91. В треугольнике ABC точка O является центром описанной окружности. Через вершину B проведена прямая, перпендикулярная AO и пересекающая AC в точке K, а через вершину C проведена прямая, также перпендикулярная AO и пересекающая AB в точке M. Найдите BC, если BK=a, CM=b.

#задача

Онлайн-тест для 8 класса. Подобие треугольников.

#тест

Привет, спасибо что читаете.

После опроса появилось несколько нововведений, давайте я о них расскажу.

Уже появились геометрические картинки, посты о геометрии. Скоро мы начнем публиковать условия задач еще и на английском языке. В июне проведем олимпиаду. Реклама в канале однажды появится, обещаю не рекламировать что попало.

Есть также далекие планы:
• Создадим бота, который будет находить задачи: случайные задачи, задачи об окружностях, задачи для 8 класса.
• Нарисуем собственный фирменный стикер-пак. Почему бы и нет?
• В новом учебном году будем публиковать готовые подборки задач к уроку. По таким урокам можно учиться или проводить уроки.

Оставайтесь с нами. Расскажите всем про канал. Правильная ссылка в других соцсетях: t.me/geometrykanal.

Всегда рада с вами пообщаться. Наташа. @natnetint