Решение задачи 91.

#решение

92. Биссектриса угла C треугольника ABC делит сторону AB на отрезки равные a и b. Касательная к окружности, описанной около треугольника ABC, проходящая через C, пересекает прямую AB в точке D. Найдите CD.

#задача

Картинка 6. Теорема о проекции.

#картинка

Решение задачи 92.

#решение

93. В четырехугольнике ABCD ∠CAD+∠BCA=180° и AB=BC+AD. Докажите, что ∠BAC+∠ACD=∠CDA.

Картинка 7. Центр окружности С_2 расположен на окружности С_1. Касательная PR к первому кругу равна их общей хорде.

#картинка

Александр Шаповалов провел 11 занятий для шестиклассников в «Сириусе», адаптируя листки для 7 класса.

Листок «Точки и прямые» в pdf
Полная коллекция листков

#занятие

Решение задачи 93.

#решение

94. Треугольник ABC — равнобедренный, ∠BAC=120°. На продолжении стороны AС за вершину A взята точка D так, что AD=2·AB. Докажите, что треугольник BDC — также равнобедренный.

#задача

Картинка 8. Выделение полного квадрата.

#картинка

Решение задачи 94.

#решение

95. В треугольниках АВС и A_1B_1C_1:
∠А = ∠А_1;
равны высоты, проведенные из вершин В и В_1;
равны медианы, проведенные из вершин С и С_1.

Обязательно ли эти треугольники равны?

#задача

Решение задачи 95.

#решение

Картинка 9.
#картинка

96. На стороне ВС равностороннего треугольника АВС отмечены точки K и L так, что BK = KL = LC, а на стороне АС отмечена точка М так, что АМ = 1/3 AC. Найдите сумму углов AKM и ALM.

#задача

Картинка 10. Ещё одно тождество с площадями

#картинка

Картинка 11 Тождество Диофанта
#картинка

Картинка 12. Объём усечённой пирамиды. (Задача 14 из Московского папируса, ок. 1850 до н.э.)

#картинка

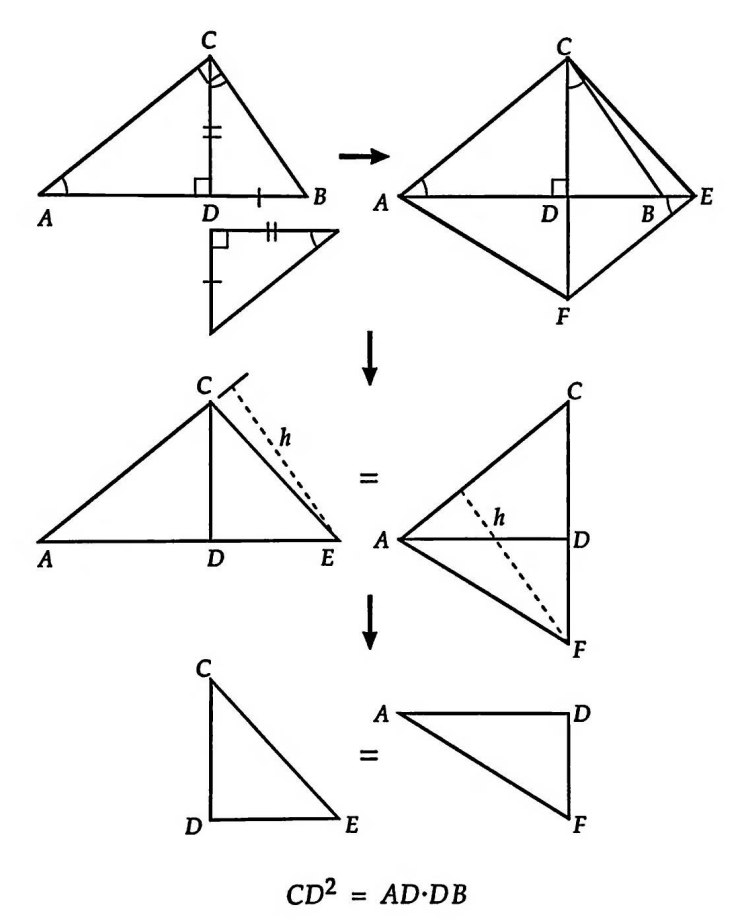
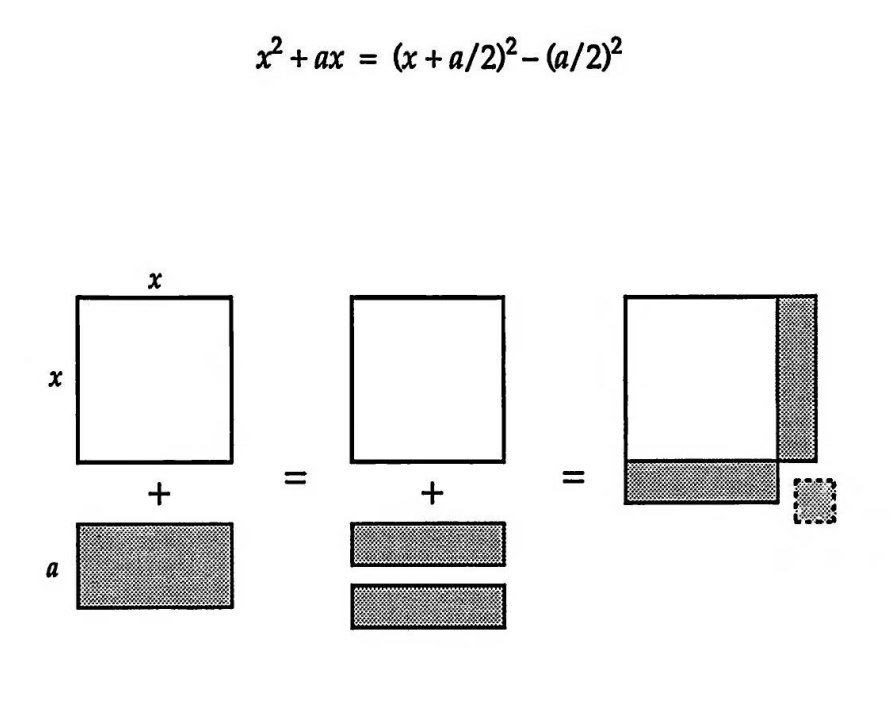
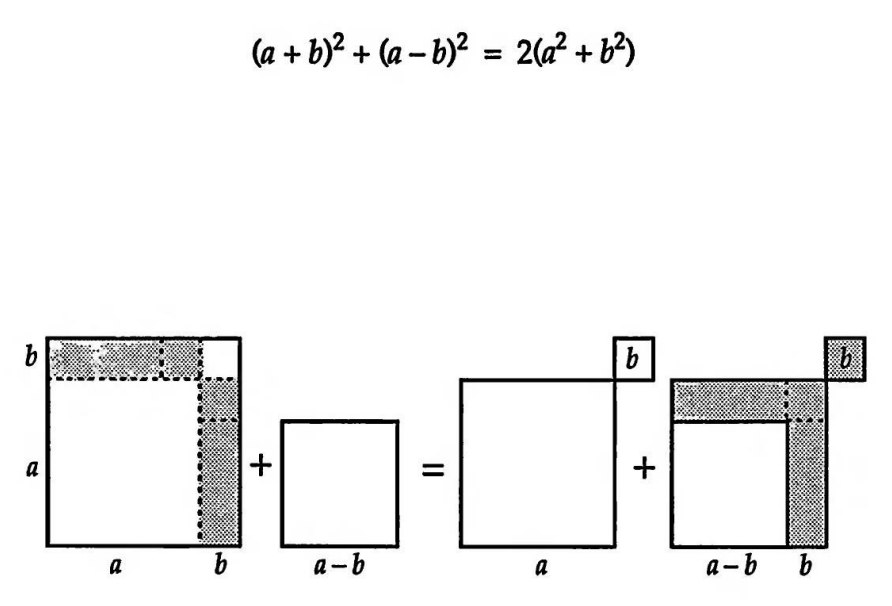
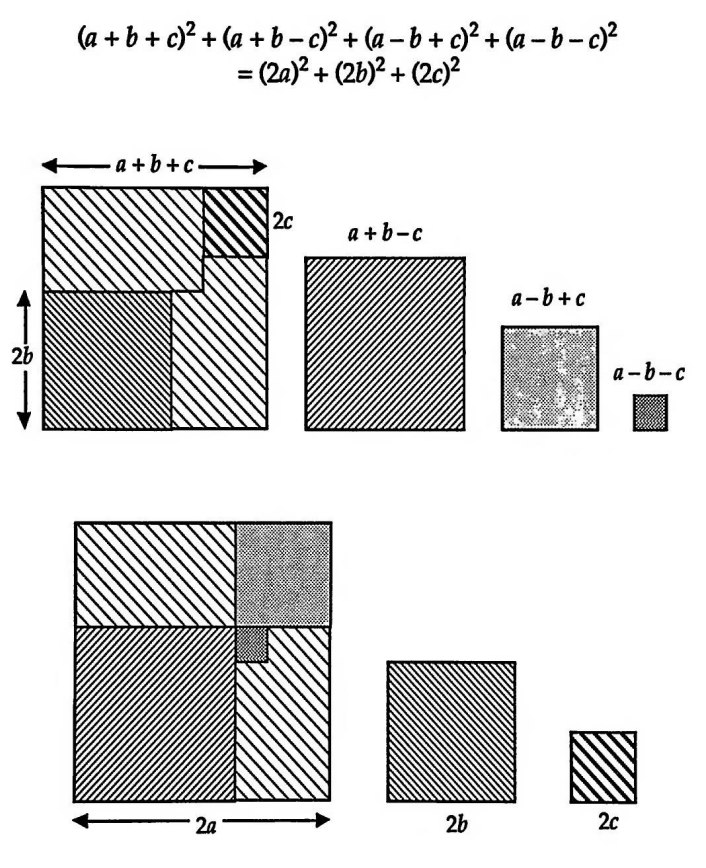
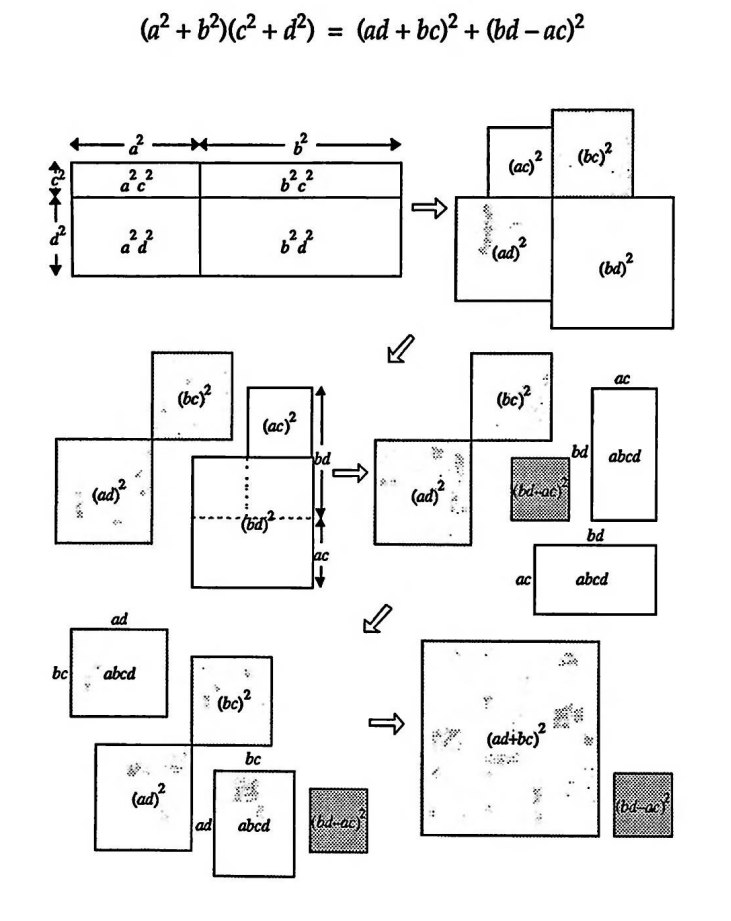
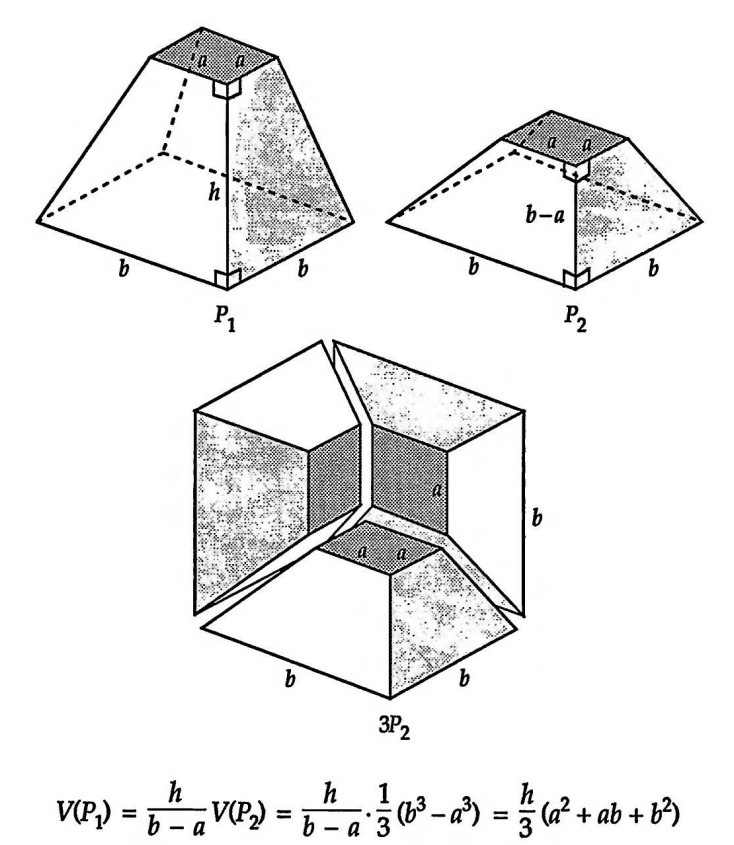
На этой неделе будем решать задачи на восстановление треугольника. Обратите внимание — не на построение, а на восстановление.

Вот общая постановка таких задач: в треугольнике отметили некоторые точки, а потом треугольник стёрли. Восстановить (с помощью циркуля и линейки) треугольник по отмеченным точкам?

Вначале предложим вашему вниманию задачи средней трудности:

Задача 97. (A, O, H) — эта запись значит: восстановить треугольник по вершине A, центру описанной окружности O и по ортоцентру H.

#задача

Решение задачи 96.

#решение