Картинка 19. Площадь треугольника S=pr.

#картинка

103. (M, H₁, L₁). Восстановить треугольник по центроиду (точке пересечения медиан), основанию H₁ высоты из вершины A и основанию L₁ биссектрисы из той же вершины.

#задача

Решение задачи 103.

#решение

Картинка 20. Сумма квадратов. На эту тему есть замечательное видео на не менее замечательном сайте математических этюдов:
http://www.etudes.ru/ru/models/sumofsquares/

#картинка

104. (M1, M2, H). Восстановите треугольник по основаниям двух медиан и ортоцентру.

#задача

Катртинка 21. Графики функций.

#картинка

Задача 105. (M₁, H₂, L₁). Восстановить треугольник по основаниям медианы и биссектрисы, проведённым из одной вершины, и основанию высоты, проведённой из другой вершины.

#задача

Решение задачи 104.

#решение

Желающие поговорить о геометрии, заходите в чатик: https://t.me/joinchat/AAAAAEQLinfWzty132-rfQ

Задача 106. (H₁, H₂, L₁). Восстановить треугольник по основаниям высоты и биссектрисы, проведённым из одной вершины, и основанию высоты, проведённой из другой вершины.

#задача

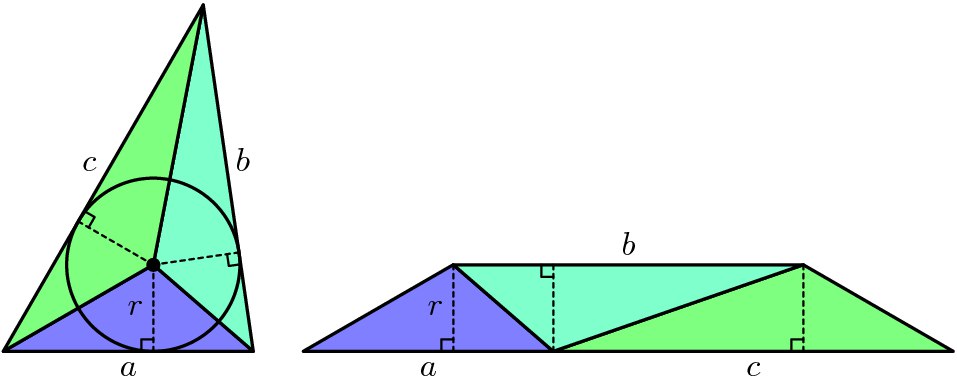
Начнём сначала. Вначале был журнал «Математика в школе». И вот однажды, в 1937 году, в его №5-6 была опубликована статья В. В. Фурсенко с длинным названием «Лексикографическое изложение конструктивных задач геометрии треугольника». В этой статье Фурсенко расположил все задачи на построение треугольника в лексикографическом порядке, решил все задачи, которые имеют решение и перечислил все задачи, которые решения не имеют.

В педагогической практике известны задачи на восстановление треугольника по трём заданным точкам. В 1982 году Верник так же, как и Фурсенко в 1937-ом, составил лексигографический список задач на восстановление треугольника. Им были выбраны самые популярные точки геометрии треугольника:

A, B, C, O — вершины треугольника и центр описанной окружности;
M_a, M_b, M_c, G — середины сторон треугольника и центр масс;
H_a, H_b, H_c, H — основания высот треугольника и ортоцентр;
T_a, T_b, T_c, I — основания биссектрис треугольника и центр вписанной окружности.

(Замечу в скобках, что мне ближе другие обозначения, но эти совпадают с нижеприведёнными на картинке.)

После чего он составил список, который называется список Верника, в котором из 139 принципиально различных задач лексикографического списка имеют решение чуть больше половины — 72 задачи. Интересно, что сам Верник, не исследовал задачи на неразрешимость, а нашел решение только 65 задач (например, у него нет решения красивой задачи №43).  Расшифровка пометок в этом списке такова:

S — задача имеет решение.
U — задача не имеет решения (доказано не Верником, а последователями и, как правило, с помощью барицентрических координат).
L — (locus dependent) данные точки не могут распологаться как угодно, а лежат на некотором ГМТ.
R — (redundant) «сводящаяся» задача: положение одной из точек определяется двумя другими.

Меня, как учителя, не интересуют задачи этого списка, которые не имеют решения. Мне интересны только те задачи, про которые известно, что у них решение есть. Как было отмечено выше, таких 72 штуки. На сегодняшний день мне не поддаются три задачи этого списка:

№57: (A, H, I),
№82: (O, T_a, I),
№131: (H_a, H, I).
Буду очень признателен всем, кто знает как решить эти задачи. Разумеется, имеется в виду и интересны только синтетические (чисто геометрические) решения — чистые доказательства существования, например, в барицентрических координатах — не предлагать. Исследование на количество решений не интересует — важно получить хотя бы одно.

Я весьма признателен Григорию Борисовичу Филлиповскому за то, что он познакомил меня с этими задачами и научил решать задачу №43 списка Верника.

Собственно список Верника.

#картинка

А вот моя статья из «Математического просвещения», в которой решены все разрешимые задачи на восстановление треугольника (за исключением вышеперечисленных), рассмотрена история вопроса, задачи на восстановление классифицированы и предложены навигаторы для учителя и для решающего по номеру задачи, по трудности и по идее решения.

#статья

«Математика в школе», 1937 №5. Тот самый номер. Скачивайте. Здесь решены все (ещё раз — внимание! — ВСЕ!!! задачи на построение треугольника).

#книга

«Математика в школе», 1937 №6.

#книга

Решение задачи 105.

#решение

Картинка 22. Разбиение правильного треугольника на 5 равных частей.
Автор: Михаил Патракеев

#картинка