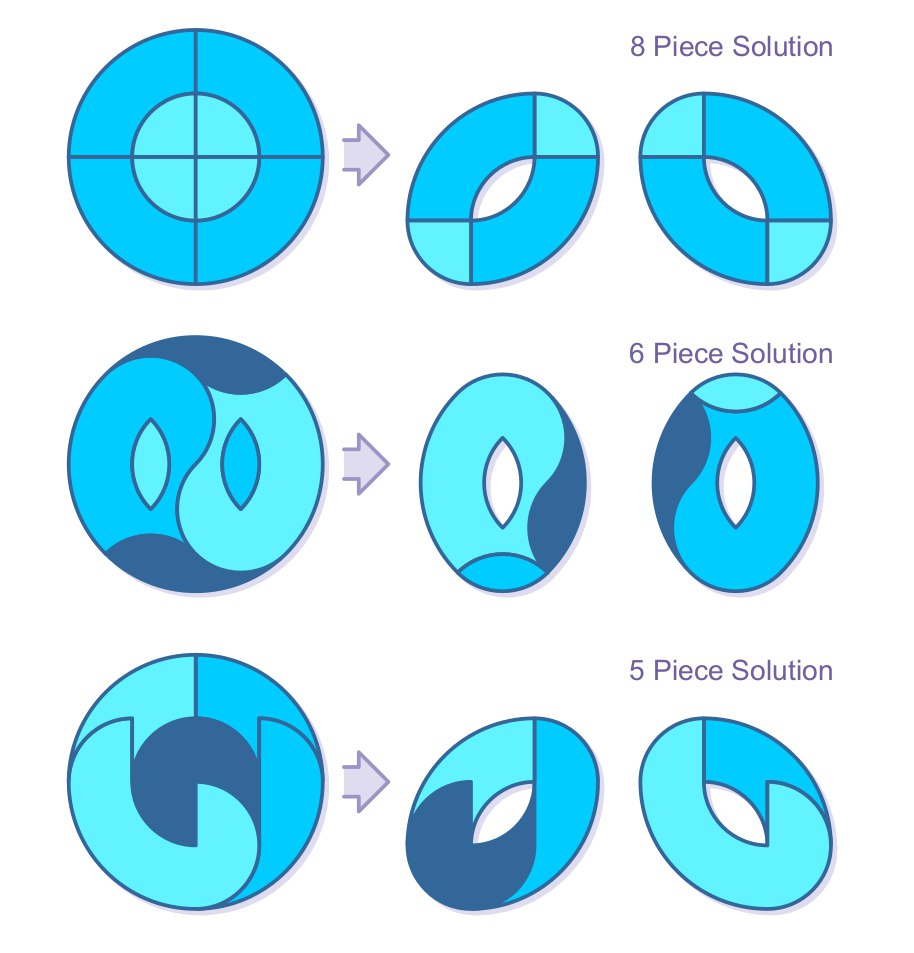
Грядущая неделя объявляется неделей задач на разрезание. Преимущественно средней и высокой сложности.
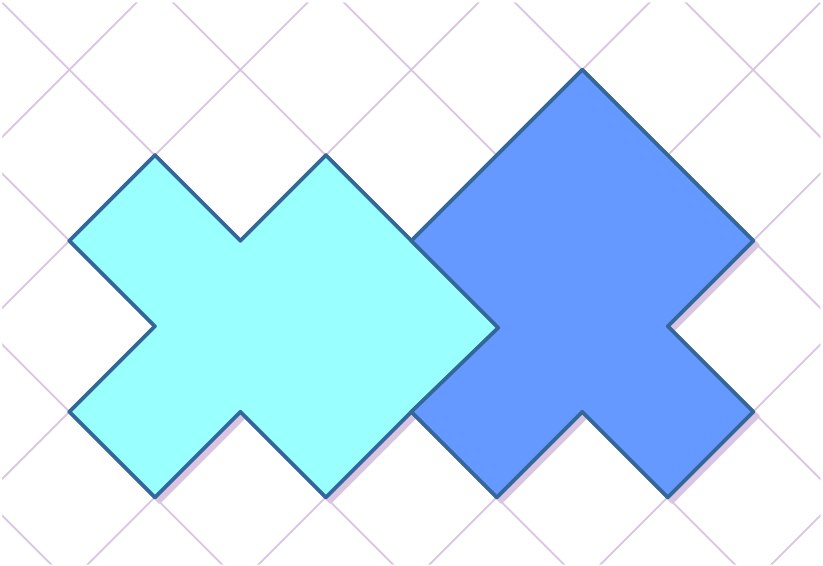
122. Из квадрата вырезали равнобедренный треугольник с вершиной в центре квадрата, как на рисунке. Разрезать эту фигуру на 4 равные части (конгруэнтные; равные по площади и форме; совпадающие при наложении).
#картинка #задача